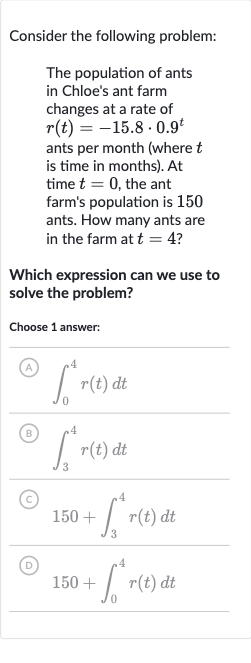
Consider the following problem: $\newline$ The population of ants in Chloe's ant farm changes at a rate of $r(t)=-15.8 \cdot 0.9^{t}$ ants per month (where $t$ is time in months). At time $t=0$ , the ant farm's population is $150$ ants. How many ants are in the farm at $t=4$ ? $\newline$ Which expression can we use to solve the problem? $\newline$ Choose $1$ answer: $\newline$ (A) $\int_{0}^{4} r(t) d t$ $\newline$ (B) $\int_{3}^{4} r(t) d t$ $\newline$ (C) $150+\int_{3}^{4} r(t) d t$ $\newline$ (D) $150+\int_{0}^{4} r(t) d t$

View step-by-step help

Home

Math Problems

Grade 8

Divide numbers written in scientific notation

Full solution

Q. Consider the following problem:

\newline

The population of ants in Chloe's ant farm changes at a rate of

r(t)=-15.8 \cdot 0.9^{t}

ants per month (where

t

is time in months). At time

t=0

, the ant farm's population is

150

ants. How many ants are in the farm at

t=4

\newline

Which expression can we use to solve the problem?

\newline

Choose

1

answer:

\newline

(A)

\int_{0}^{4} r(t) d t

\newline

(B)

\int_{3}^{4} r(t) d t

\newline

(C)

150+\int_{3}^{4} r(t) d t

\newline

(D)

150+\int_{0}^{4} r(t) d t

Initial Population and Rate Function: To find the number of ants at $t=4$ , we need to account for the initial population and the change in population over time. The initial population is given as $150$ ants at $t=0$ . The rate of change of the population is given by the function $r(t)=-15.8\times 0.9^{t}$ . To find the total change in population from $t=0$ to $t=4$ , we need to integrate the rate function over this interval.
Definite Integral Calculation: We will use the definite integral to calculate the total change in population from $t=0$ to $t=4$ . The integral of the rate function $r(t)$ over the interval from $0$ to $4$ will give us the net change in the population during this time period.
Total Number of Ants at $t=4$ : The correct expression to calculate the total number of ants at $t=4$ is the initial population plus the integral of the rate function from $t=0$ to $t=4$ . Mathematically, this is represented as: $\newline$ $150 + \int_{0}^{4}r(t)\,dt$
Correct Choice Explanation: Looking at the given options, we can see that option (D) matches the expression we derived: $\newline$ (D) $150 + \int_{0}^{4}r(t)dt$ $\newline$ This is the correct choice because it starts with the initial population and adds the change in population from $t=0$ to $t=4$ .
Incorrect Options Explanation: To confirm, options $(A)$ , $(B)$ , and $(C)$ are incorrect because: $\newline$ $(A)$ does not include the initial population. $\newline$ $(B)$ starts integrating from $t=3$ , which would not account for the change from $t=0$ to $t=3$ . $\newline$ $(C)$ includes the initial population but starts integrating from $t=3$ , which also does not account for the change from $t=0$ to $t=3$ .