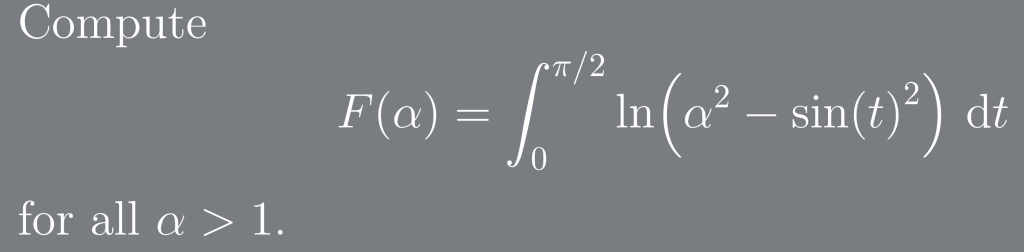Compute F(alpha)=int_(0)^(pi//2)ln(alpha^(2)-sin(t)^(2))dt for all alpha 1.

Question

Compute  F(alpha)=int_(0)^(pi//2)ln(alpha^(2)-sin(t)^(2))dt for all  alpha > 1.

Bytelearn · Accepted Answer

Rephrase the Problem: First, let's rephrase the  ＂Evaluate the integral of the natural logarithm of alpha squared minus the square of the sine of t from 0 to pi/2, where alpha is greater than 1.＂Given Integral: We are given the integral to compute: F(alpha) = ∫ from 0 to pi/2 of ln(alpha^2 - sin^2(t)) dt, where alpha > 1.Properties Consideration: To solve this integral, we need to consider the properties of the natural logarithm and the bounds of integration. Since alpha > 1, alpha^2 - sin^2(t) is always positive within the bounds of integration, ensuring the natural logarithm is defined.Trigonometric Identity: We can't directly integrate ln(alpha^2 - sin^2(t)) dt, so we need to look for a substitution or a property that can simplify the integral. One approach is to use the trigonometric identity sin^2(t) = (1 - cos(2t))/2 to rewrite the integrand.Apply Identity: Applying the trigonometric identity, we get: ln(alpha^2 - sin^2(t)) = ln(alpha^2 - (1 - cos(2t))/2).Simplify Expression: Simplify the expression inside the logarithm: ln(alpha^2 - (1 - cos(2t))/2) = ln((2alpha^2 - 1 + cos(2t))/2).Rewrite Integral: Now, we can rewrite the integral with the simplified integrand: F(alpha) = ∫ from 0 to pi/2 of ln((2alpha^2 - 1 + cos(2t))/2) dt.Consider Symmetry: However, this integral still does not have an elementary antiderivative. We need to consider if there are any symmetries or other properties that can help us evaluate the integral. One such property is the evenness of the cosine function, which might suggest a symmetry in the interval [0, pi/2].Complex Integral: Unfortunately, the presence of the natural logarithm complicates the use of symmetry directly. At this point, we realize that the integral does not have a simple closed-form solution in terms of elementary functions, and it might require special functions or numerical methods to evaluate.Conclusion: Since the integral cannot be evaluated using elementary functions, we conclude that the problem cannot be solved in the form requested. We must either leave the integral as it is or use numerical methods to approximate the value of F(alpha) for alpha > 1.

Compute $\newline$ $F(\alpha)=\int_{0}^{\pi/2}\ln(\alpha^{2}-\sin(t)^{2})dt$ $\newline$ for all \alpha > 1.

Full solution

More problems from Evaluate definite integrals using the chain rule

Related topics

Compute\newlineF(α)=∫0π/2ln⁡(α2−sin⁡(t)2)dtF(\alpha)=\int_{0}^{\pi/2}\ln(\alpha^{2}-\sin(t)^{2})dtF(α)=∫0π/2​ln(α2−sin(t)2)dt\newlinefor all \alpha > 1.

Compute $\newline$ $F(\alpha)=\int_{0}^{\pi/2}\ln(\alpha^{2}-\sin(t)^{2})dt$ $\newline$ for all \alpha > 1.