Full solution
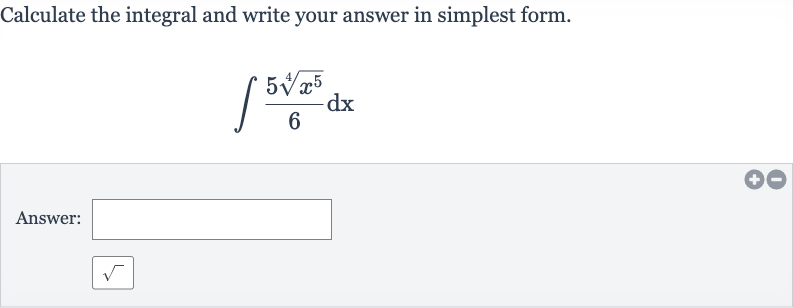
Q. Calculate the integral and write your answer in simplest form.Answer:
- Rewrite in Exponents: We are given the integral to solve:First, we rewrite the integral in terms of exponents to simplify the integration process.So the integral becomes:
- Pull Out Constant Factor: Now we can pull out the constant factor from the integral:
- Apply Power Rule: Next, we apply the power rule for integration, which states that:where and is the constant of integration. For our integral, , so we get:
- Simplify Exponent and Fraction: We simplify the exponent and the fraction:So the integral becomes:
- Multiply by Reciprocal: To simplify the fraction, we multiply by the reciprocal of :
- Multiply Constants: Now we multiply the constants:
- Simplify Fraction: We can simplify the fraction by dividing both the numerator and the denominator by their greatest common divisor, which is :So the integral simplifies to: