Full solution
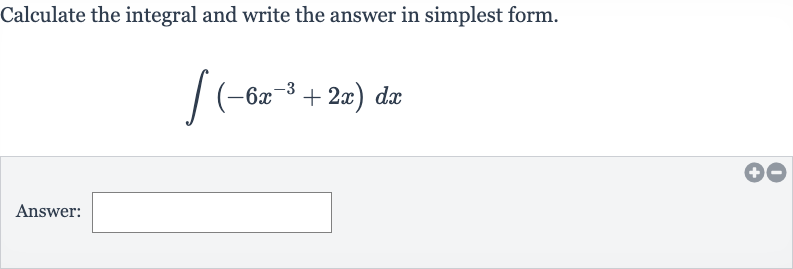
Q. Calculate the integral and write the answer in simplest form.Answer:
- Identify Integral: Identify the integral to be solved.We need to integrate the function with respect to .
- Break Down Integral: Break down the integral into two separate integrals.The integral of a sum of functions is the sum of the integrals of each function, so we can write:\int(\(-6x^{} + x)\,dx = \int(x^{})\,dx + \int(x)\,dx
- Integrate First Part: Integrate the first part of the function, . The integral of with respect to is , where . Applying this rule:
- Integrate Second Part: Integrate the second part of the function, . Using the same rule as before:
- Combine Results: Combine the results of the two integrals.The combined result of the integrals is:Since and are both constants, we can combine them into a single constant .Final result: