Full solution
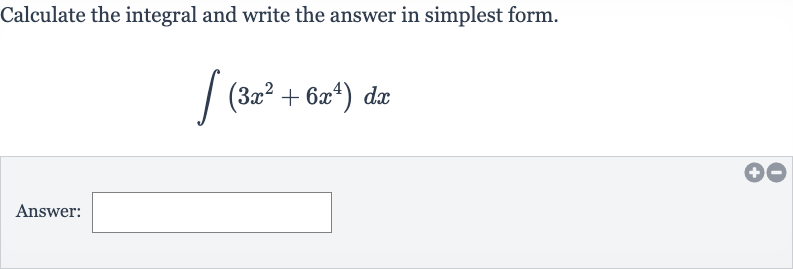
Q. Calculate the integral and write the answer in simplest form.Answer:
- Integrate : We are given the integral of a polynomial function. To solve this, we will integrate each term separately using the power rule for integration, which states that the integral of with respect to is for any real number .Let's integrate the first term :
- Integrate : Now, let's integrate the second term :
- Combine integrals: Combine the results of the two integrals to get the final indefinite integral:where is the constant of integration.