Full solution
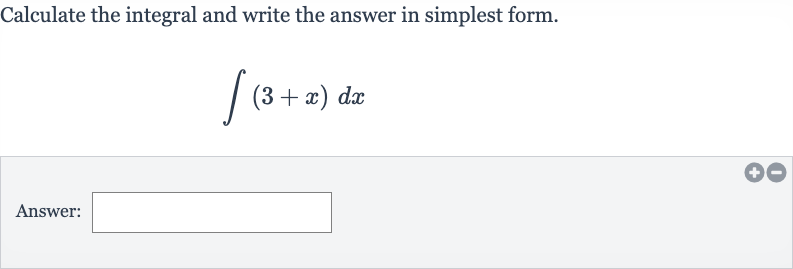
Q. Calculate the integral and write the answer in simplest form.Answer:
- Split Function: We need to find the indefinite integral of the function with respect to . The integral of a sum is the sum of the integrals, so we can integrate and separately.
- Integrate Constant: First, we integrate the constant with respect to . The integral of a constant with respect to is , so:
- Integrate Variable: Next, we integrate with respect to . The integral of with respect to is , because the power rule for integration states that for .
- Combine Results: Now, we combine the results of the two integrals and add the constant of integration , since this is an indefinite integral.