Full solution
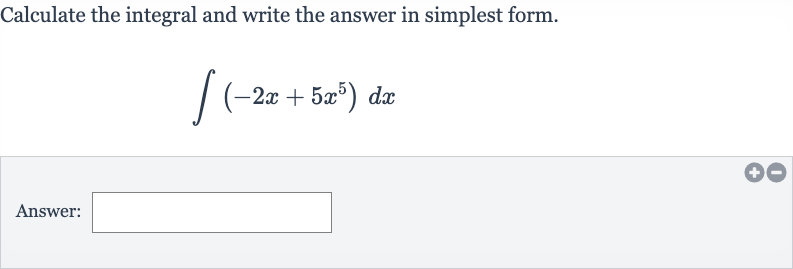
Q. Calculate the integral and write the answer in simplest form.Answer:
- Identify integral function: Identify the integral to be solved.We need to integrate the function with respect to .
- Apply power rule: Apply the power rule for integration to each term separately.The power rule for integration states that , where is the constant of integration.For the first term, , we have , so the integral is .For the second term, , we have , so the integral is .
- Perform integration: Perform the integration for each term.For the first term, , the integral is .For the second term, , the integral is .
- Combine results: Combine the results of the integrals and add the constant of integration. The combined integral is , where is the constant of integration.