AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
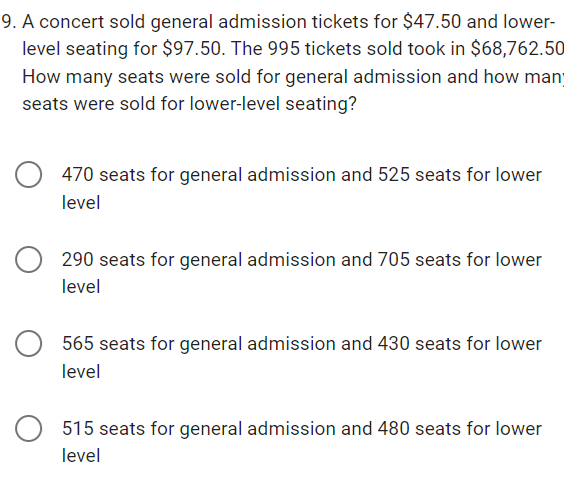
A concert sold general admission tickets for and lowerlevel seating for . The tickets sold took in How many seats were sold for general admission and how man seats were sold for lower-level seating? seats for general admission and seats for lower level seats for general admission and seats for lower level seats for general admission and seats for lower level seats for general admission and seats for lower level
Full solution
Q. A concert sold general admission tickets for and lowerlevel seating for . The tickets sold took in How many seats were sold for general admission and how man seats were sold for lower-level seating? seats for general admission and seats for lower level seats for general admission and seats for lower level seats for general admission and seats for lower level seats for general admission and seats for lower level
- Define variables: Let's define variables: Let be the number of general admission tickets and be the number of lower-level seating tickets.
- Write equations: Write the equations based on the total number of tickets and the total revenue. Equation : (total tickets). Equation : (total revenue).
- Solve first equation: Solve the first equation for : .
- Substitute and simplify: Substitute in the second equation: .
- Solve for y: Simplify and solve for : . Combine like terms: . Then, .
- Substitute for x: Substitute back into the equation for : , so .
- Check solution: Check the solution by substituting and back into the original revenue equation: .
More problems from Solve a system of equations using substitution: word problems
QuestionGet tutor help
QuestionGet tutor help
