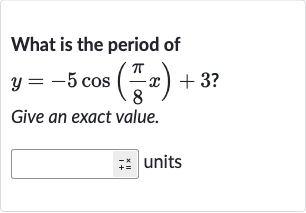AI tutor
Full solution
Q. What is the period ofGive an exact value.units
- Identify Standard Form: Identify the standard form of a cosine function and its period.The standard form of a cosine function is , where:- is the amplitude,- affects the period of the function,- is the phase shift, and- is the vertical shift.The period of the standard cosine function is . For the function , the period is given by the formula .
- Determine Value of B: Determine the value of B in the given function.In the given function , the value of B is .
- Calculate Period: Calculate the period of the given function using the formula.Using the formula , we substitute with :.
More problems from Solve a system of equations using any method
QuestionGet tutor help
QuestionGet tutor help