Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Ishaan is 2 times as old as Christopher. 35 years ago, Ishaan was 7 times as old as Christopher. How old is Christopher now?

Ishaan is \(2\) times as old as Christopher. \(35\) years ago, Ishaan was \(7\) times as old as Christopher.\newlineHow old is Christopher now?

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Solve a system of equations using any method: word problemsright chevron icon

Full solution

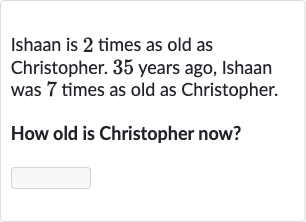
Q. Ishaan is \(2\) times as old as Christopher. \(35\) years ago, Ishaan was \(7\) times as old as Christopher.\newlineHow old is Christopher now?
  1. Denoting Ages: Let's denote Christopher's current age as cc and Ishaan's current age as ii. According to the problem, Ishaan is 22 times as old as Christopher.\newlineFirst equation: i=2ci = 2c
  2. First Equation: 3535 years ago, Ishaan's age was i−35i - 35 and Christopher's age was c−35c - 35. According to the problem, at that time, Ishaan was 77 times as old as Christopher.\newlineSecond equation: i−35=7(c−35)i - 35 = 7(c - 35)
  3. Second Equation: Now we have a system of two equations:\newline11) i=2ci = 2c\newline22) i−35=7(c−35)i - 35 = 7(c - 35)\newlineWe can substitute the value of ii from the first equation into the second equation to find cc.
  4. Substituting ii into the Second Equation: Substituting i=2ci = 2c into the second equation:\newline2c−35=7(c−35)2c - 35 = 7(c - 35)\newlineExpanding the equation:\newline2c−35=7c−2452c - 35 = 7c - 245
  5. Expanding the Equation: Now, let's solve for cc:
    2c−7c=−245+352c - 7c = -245 + 35
    −5c=−210-5c = -210
    c=−210−5c = \frac{-210}{-5}
    c=42c = 42
  6. Solving for c: We found that Christopher's current age is 4242 years old. Now let's check if this satisfies the original conditions.\newlineIshaan's current age would be 2×42=842 \times 42 = 84 years old.\newline3535 years ago, Christopher was 42−35=742 - 35 = 7 years old, and Ishaan was 84−35=4984 - 35 = 49 years old.\newlineIndeed, 4949 is 77 times 77, so the conditions are satisfied.

More problems from Solve a system of equations using any method: word problems

Question
Solve using substitution. 5x−2y=−7 5x - 2y = -7 x=−5 x = -5 (_,_)
Get tutor helpright-arrow

Posted 5 months ago

Question
Is (1,1)(1,1) a solution to this system of equations? \newline4x+10y=144x + 10y = 14\newlinex+6y=7x + 6y = 7\newlineChoices:\newline(A) yes \newline(B) no
Get tutor helpright-arrow

Posted 5 months ago

Question
Which describes the system of equations below?\newliney=–3x+9y = –3x + 9 \newliney=–3x+9y = –3x + 9 \newlineChoices:\newline(A) consistent and independent\text{(A) consistent and independent} \newline(B) consistent and dependent\text{(B) consistent and dependent} \newline(C) inconsistent\text{(C) inconsistent}
Get tutor helpright-arrow

Posted 5 months ago

Question
Solve using elimination. \newline7x−8y=−17 7x - 8y = -17 \newline −7x+3y=2 -7x + 3y = 2 \newline (____,____)(\_\_\_\_, \_\_\_\_)
Get tutor helpright-arrow

Posted 5 months ago

Question
Solve. \newlinex=−2 x = -2 \newline−2x+2y=−8 -2x + 2y = -8 \newline(____,____)(\_\_\_\_, \_\_\_\_)
Get tutor helpright-arrow

Posted 9 months ago

Question
Write a system of equations to describe the situation below, solve using any method, and fill in the blanks.\newlineAt a community barbecue, Mrs. Wilkerson and Mr. Hogan are buying dinner for their families. Mrs. Wilkerson purchases 33 hot dog meals and 33 hamburger meals, paying a total of $36\$36. Mr. Hogan buys 11 hot dog meal and 33 hamburger meals, spending $26\$26 in all. How much do the meals cost?\newlineHot dog meals cost $\$_______ each, and hamburger meals cost $\$________ each.
Get tutor helpright-arrow

Posted 9 months ago

Question
Solve the system of equations by substitution.\newline−3x−y−3z=−11-3x - y - 3z = -11\newlinez=5z = 5\newlinex−y+3z=19x - y + 3z = 19\newline(____.____,____)
Get tutor helpright-arrow

Posted 5 months ago

Question
Solve the system of equations by elimination.\newlinex−3y−2z=10 x - 3y - 2z = 10 \newline3x+2y+2z=14 3x + 2y + 2z = 14 \newline2x−3y−2z=16 2x - 3y - 2z = 16 \newline(_,_,_)(\_,\_,\_)
Get tutor helpright-arrow

Posted 5 months ago

Question
Solve the system of equations.\newliney=x2+36x+3 y = x^2 + 36x + 3 \newliney=22x−37 y = 22x - 37 \newlineWrite the coordinates in exact form. Simplify all fractions and radicals.\newline(_,_)(\_,\_)\newline(_,_)(\_,\_)
Get tutor helpright-arrow

Posted 5 months ago

Question
Solve the system of equations.\newliney=−x−24 y = -x - 24 \newlinex2+y2=488 x^2 + y^2 = 488 \newlineWrite the coordinates in exact form. Simplify all fractions and radicals.\newline(_,_) (\_,\_) \newline(_,_) (\_,\_)
Get tutor helpright-arrow

Posted 5 months ago

View all (92)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant