Full solution
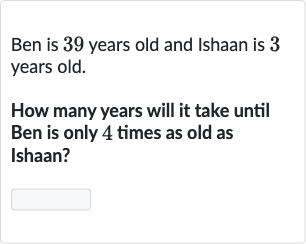
Q. Ben is \(39\) years old and Ishaan is \(3\) years old.How many years will it take until Ben is only \(4\) times as old as Ishaan?
- Denoting the number of years: Let's denote the number of years it will take for Ben to be only times as old as Ishaan as . Currently, Ben is years old and Ishaan is years old. After years, Ben will be years old and Ishaan will be years old. The equation to represent the situation where Ben is times as old as Ishaan is:
- Distributing the on the right side: Now, let's distribute the on the right side of the equation:
- Rearranging the equation to solve for n: Next, we will rearrange the equation to solve for "n". Let's subtract "n" from both sides of the equation:
- Isolating the term with n: Now, we will subtract from both sides to isolate the term with "n":
- Dividing both sides to solve for : Finally, we will divide both sides by to solve for :
More problems from Solve a system of equations using any method: word problems
QuestionGet tutor help
QuestionGet tutor help