Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

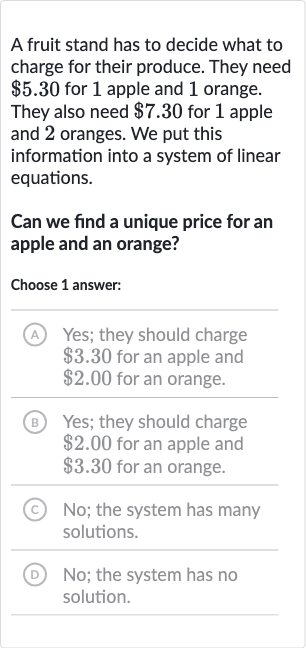
A fruit stand has to decide what to charge for their produce. They need $5.30 for 1 apple and 1 orange. They also need $7.30 for 1 apple and 2 oranges. We put this information into a system of linear equations. Can we find a unique price for an apple and an orange? Choose 1 answer: (A) Yes; they should charge $3.30 for an apple and $2.00 for an orange. (B) Yes; they should charge $2.00 for an apple and $3.30 for an orange. (C) No; the system has many solutions. (D) No; the system has no solution.

A fruit stand has to decide what to charge for their produce. They need $5.30 \$ 5.30 for 11 apple and 11 orange. They also need $7.30 \$ 7.30 for 11 apple and 22 oranges. We put this information into a system of linear equations.\newlineCan we find a unique price for an apple and an orange?\newlineChoose 11 answer:\newline(A) Yes; they should charge $3.30 \$ 3.30 for an apple and $2.00 \$ 2.00 for an orange.\newlineB Yes; they should charge $2.00 \$ 2.00 for an apple and $3.30 \$ 3.30 for an orange.\newline(C) No; the system has many solutions.\newline(D) No \mathrm{No} ; the system has no solution.

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Solve a system of equations using any method: word problemsright chevron icon

Full solution

Q. A fruit stand has to decide what to charge for their produce. They need $5.30 \$ 5.30 for 11 apple and 11 orange. They also need $7.30 \$ 7.30 for 11 apple and 22 oranges. We put this information into a system of linear equations.\newlineCan we find a unique price for an apple and an orange?\newlineChoose 11 answer:\newline(A) Yes; they should charge $3.30 \$ 3.30 for an apple and $2.00 \$ 2.00 for an orange.\newlineB Yes; they should charge $2.00 \$ 2.00 for an apple and $3.30 \$ 3.30 for an orange.\newline(C) No; the system has many solutions.\newline(D) No \mathrm{No} ; the system has no solution.
  1. Define Prices: Let's define the price of an apple as AA and the price of an orange as OO. We can then translate the given information into two equations:\newline11 apple + 11 orange = $(5.30)\$(5.30)\newline11 apple + 22 oranges = $(7.30)\$(7.30)\newlineThis can be written as the system of linear equations:\newlineA+O=5.30A + O = 5.30\newlineA+2O=7.30A + 2O = 7.30
  2. Use Elimination Method: To solve this system, we can use the method of substitution or elimination. Let's use elimination. We'll subtract the first equation from the second to eliminate AA and find the price of an orange.(A+2O)−(A+O)=7.30−5.30(A + 2O) - (A + O) = 7.30 - 5.30This simplifies to:2O−O=2.002O - O = 2.00O=2.00O = 2.00
  3. Substitute to Find Apple Price: Now that we have the price of an orange, we can substitute it back into the first equation to find the price of an apple.\newlineA+O=5.30A + O = 5.30\newlineA+2.00=5.30A + 2.00 = 5.30\newlineSubtracting 2.002.00 from both sides gives us:\newlineA=5.30−2.00A = 5.30 - 2.00\newlineA=3.30A = 3.30
  4. Final Prices: We have found unique prices for both an apple and an orange:\newlineA (apple) = $3.30\$3.30\newlineO (orange) = $2.00\$2.00\newlineThis corresponds to answer choice (A)(A).

More problems from Solve a system of equations using any method: word problems

Question
Solve using substitution. 5x−2y=−7 5x - 2y = -7 x=−5 x = -5 (_,_)
Get tutor helpright-arrow

Posted 5 months ago

Question
Is (1,1)(1,1) a solution to this system of equations? \newline4x+10y=144x + 10y = 14\newlinex+6y=7x + 6y = 7\newlineChoices:\newline(A) yes \newline(B) no
Get tutor helpright-arrow

Posted 5 months ago

Question
Which describes the system of equations below?\newliney=–3x+9y = –3x + 9 \newliney=–3x+9y = –3x + 9 \newlineChoices:\newline(A) consistent and independent\text{(A) consistent and independent} \newline(B) consistent and dependent\text{(B) consistent and dependent} \newline(C) inconsistent\text{(C) inconsistent}
Get tutor helpright-arrow

Posted 5 months ago

Question
Solve using elimination. \newline7x−8y=−17 7x - 8y = -17 \newline −7x+3y=2 -7x + 3y = 2 \newline (____,____)(\_\_\_\_, \_\_\_\_)
Get tutor helpright-arrow

Posted 5 months ago

Question
Solve. \newlinex=−2 x = -2 \newline−2x+2y=−8 -2x + 2y = -8 \newline(____,____)(\_\_\_\_, \_\_\_\_)
Get tutor helpright-arrow

Posted 9 months ago

Question
Write a system of equations to describe the situation below, solve using any method, and fill in the blanks.\newlineAt a community barbecue, Mrs. Wilkerson and Mr. Hogan are buying dinner for their families. Mrs. Wilkerson purchases 33 hot dog meals and 33 hamburger meals, paying a total of $36\$36. Mr. Hogan buys 11 hot dog meal and 33 hamburger meals, spending $26\$26 in all. How much do the meals cost?\newlineHot dog meals cost $\$_______ each, and hamburger meals cost $\$________ each.
Get tutor helpright-arrow

Posted 9 months ago

Question
Solve the system of equations by substitution.\newline−3x−y−3z=−11-3x - y - 3z = -11\newlinez=5z = 5\newlinex−y+3z=19x - y + 3z = 19\newline(____.____,____)
Get tutor helpright-arrow

Posted 5 months ago

Question
Solve the system of equations by elimination.\newlinex−3y−2z=10 x - 3y - 2z = 10 \newline3x+2y+2z=14 3x + 2y + 2z = 14 \newline2x−3y−2z=16 2x - 3y - 2z = 16 \newline(_,_,_)(\_,\_,\_)
Get tutor helpright-arrow

Posted 5 months ago

Question
Solve the system of equations.\newliney=x2+36x+3 y = x^2 + 36x + 3 \newliney=22x−37 y = 22x - 37 \newlineWrite the coordinates in exact form. Simplify all fractions and radicals.\newline(_,_)(\_,\_)\newline(_,_)(\_,\_)
Get tutor helpright-arrow

Posted 5 months ago

Question
Solve the system of equations.\newliney=−x−24 y = -x - 24 \newlinex2+y2=488 x^2 + y^2 = 488 \newlineWrite the coordinates in exact form. Simplify all fractions and radicals.\newline(_,_) (\_,\_) \newline(_,_) (\_,\_)
Get tutor helpright-arrow

Posted 5 months ago

View all (92)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant