AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
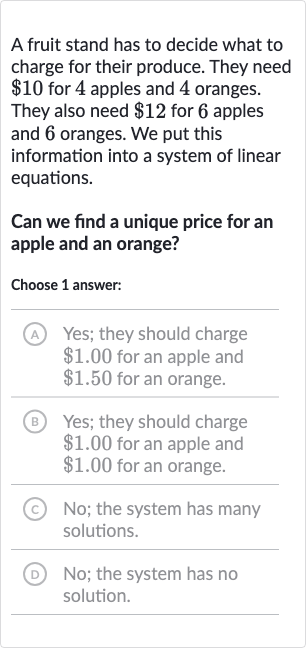
A fruit stand has to decide what to charge for their produce. They need for apples and oranges. They also need for apples and oranges. We put this information into a system of linear equations.Can we find a unique price for an apple and an orange?Choose answer:A Yes; they should charge for an apple and for an orange.B Yes; they should charge for an apple and for an orange.(C) No; the system has many solutions.(D) ; the system has no solution.
Full solution
Q. A fruit stand has to decide what to charge for their produce. They need for apples and oranges. They also need for apples and oranges. We put this information into a system of linear equations.Can we find a unique price for an apple and an orange?Choose answer:A Yes; they should charge for an apple and for an orange.B Yes; they should charge for an apple and for an orange.(C) No; the system has many solutions.(D) ; the system has no solution.
- Translate into equations: Let's denote the price of an apple as and the price of an orange as . We can then translate the information given into two equations:. .
- Simplify equations: We can simplify both equations by dividing them by their common factors to make the coefficients smaller and the equations easier to work with:. Divide the first equation by : . Divide the second equation by :
More problems from Solve a system of equations using any method: word problems
QuestionGet tutor help
QuestionGet tutor help
