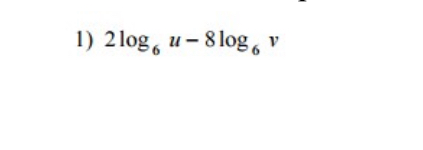AI tutor
Full solution
Q. )
- Recognize Properties: Recognize the properties of logarithms that can be applied to simplify the expression.The properties of logarithms that are relevant here are:- The Power Rule: Using this property, we can take the coefficients in front of the logarithms and turn them into exponents inside the logarithms.
- Apply Power Rule: Apply the Power Rule to the given expression.We have , which can be rewritten using the Power Rule as:
- Combine Using Quotient Rule: Combine the two logarithms into a single logarithm using the Quotient Rule.The Quotient Rule for logarithms states that .Applying this rule to our expression gives us:
- Check for Simplifications: Check for any possible simplifications of the expression inside the logarithm. In this case, there are no further simplifications that can be made to the expression .
More problems from Solve a system of equations using any method
QuestionGet tutor help
QuestionGet tutor help