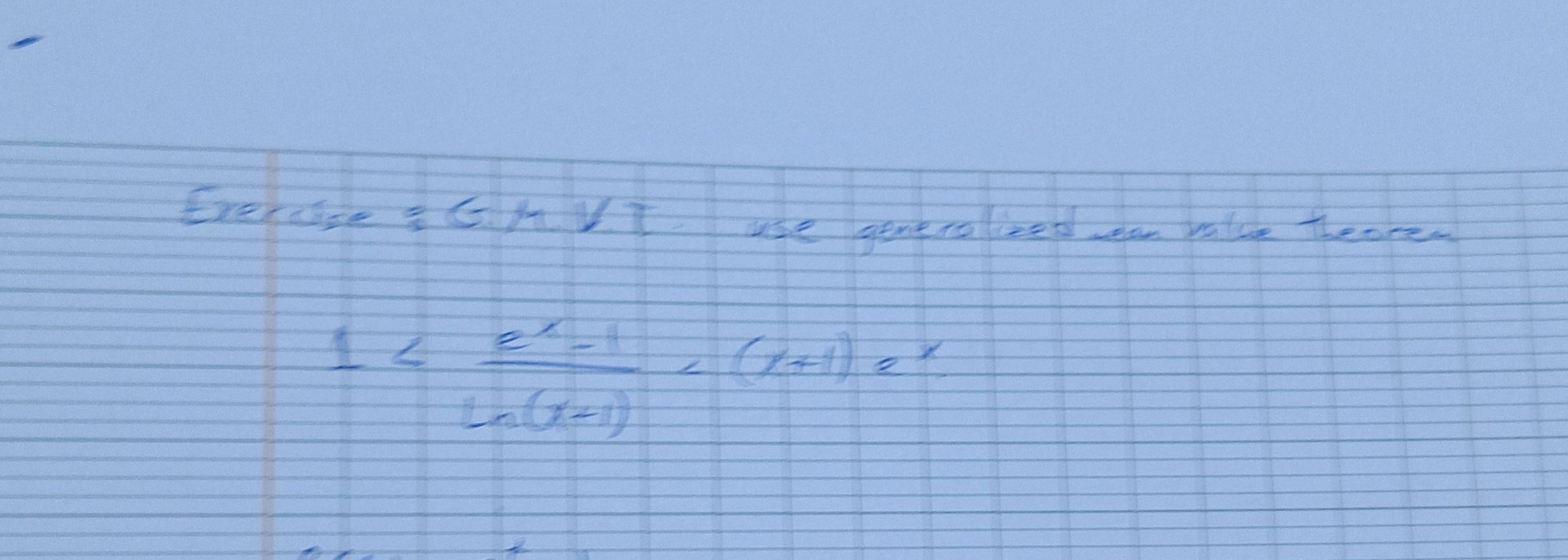Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

1 < (e^(x)-1)/(ln(x-1)) < (x+1)=x

$1<\frac{e^{x}-1}{\ln (x-1)}<(x+1)=x$

View step-by-step help

View step-by-step help

Solve advanced linear inequalities

Full solution

Q.

1<\frac{e^{x}-1}{\ln (x-1)}<(x+1)=x

Isolate exponential expression: First, let's address the inequality $1 < \frac{e^{x}-1}{\ln(x-1)}$ . We need to isolate the exponential expression on one side.
Multiply by $\ln(x-1)$ : Multiply both sides of the inequality by $\ln(x-1)$ to get rid of the denominator, assuming $\ln(x-1)$ is positive (which it must be for the logarithm to be defined and for the inequality to maintain its direction). $\newline$ $1 \cdot \ln(x-1) < e^{x} - 1$
Add $1$ to isolate $e^{x}$ : Add $1$ to both sides of the inequality to isolate $e^{x}$ . $\newline$ $\ln(x-1) + 1 < e^{x}$
Address second part of inequality: Now, let's address the second part of the inequality $(e^{x}-1)/(\ln(x-1)) < (x+1)=x$ . This seems to be a typo or a mistake because $(x+1)=x$ is not an inequality and does not make sense in this context. We will assume that the intended inequality is $(e^{x}-1)/(\ln(x-1)) < x+1$ .

More problems from Solve advanced linear inequalities

Question

-2 x+b y=59

\newline

5 x-y=1

\newline

If the system of equations has exactly one solution

(x, y)

x=2

, what is the value of

b

Posted 2 months ago

Question

\newline

\frac{\sqrt[3]{2}}{\sqrt[3]{-128}}=

Posted 7 days ago

Question

\newline

\frac{\sqrt[4]{2}}{\sqrt[4]{162}}=

Posted 3 months ago

Question

\newline

\sqrt[5]{-16} \cdot 2^{\frac{1}{5}}=

Posted 2 months ago

Question

y

\newline

\begin{array}{l} \frac{y-1}{3 y+7}=\frac{1}{10} \\ y=\square \end{array}

Posted 3 months ago

Question

x

\newline

Your answer must be simplified.

\newline

-30<\frac{x}{-4}

Posted 2 months ago

Question

x

\newline

Your answer must be simplified.

\newline

-36+x<8

Posted 2 months ago

Question

x

\newline

Your answer must be simplified.

\newline

2 x<15

Posted 3 months ago

Question

x

\newline

Your answer must be simplified.

\newline

x-6 \leq 3

Posted 1 month ago

Question

x

\newline

Your answer must be simplified.

\newline

7>\frac{x}{4}

Posted 3 months ago