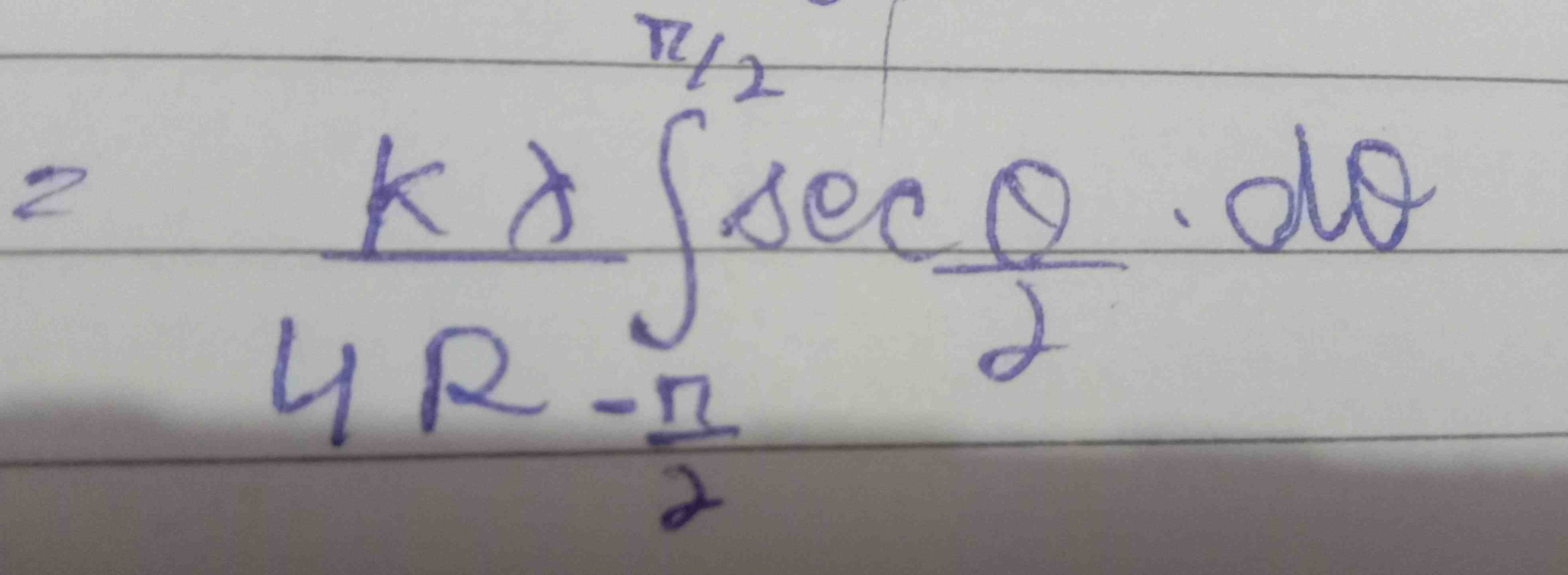Full solution

Q. Evaluate.

\newline

\frac{k \lambda}{4 R} \int_{-\frac{\pi}{2}}^{\pi / 2} \sec \frac{\theta}{2} \cdot d \theta

Identify Integral: Identify the integral that needs to be evaluated. $\newline$ We have the integral $\int_{-\left(\frac{\pi}{2}\right)}^{\frac{\pi}{2}} \sec\left(\frac{\theta}{2}\right) d\theta$ with limits from $-\left(\frac{\pi}{2}\right)$ to $\frac{\pi}{2}$ .
Simplify Integrands: Use a trigonometric identity to simplify the integrand. The secant function can be expressed as $\sec(x) = \frac{1}{\cos(x)}$ . Therefore, $\sec(\frac{\theta}{2}) = \frac{1}{\cos(\frac{\theta}{2})}$ .
Recognize Integral Rule: Recognize that the integral of $\sec(x)$ is $\ln|\sec(x) + \tan(x)| + C$ . However, since we have $\sec(\theta/2)$ , we need to adjust the integral accordingly.
Perform Substitution: Perform a substitution to integrate $\sec(\frac{\theta}{2})$ . Let $u = \frac{\theta}{2}$ , which implies $d\theta = 2du$ . We need to change the limits of integration as well. When $\theta = -\left(\frac{\pi}{2}\right)$ , $u = -\left(\frac{\pi}{4}\right)$ , and when $\theta = \frac{\pi}{2}$ , $u = \frac{\pi}{4}$ .
Rewrite in Terms of u: Rewrite the integral in terms of u. $\newline$ The integral becomes $\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \sec(u) \cdot 2\,du$ with limits from $-\frac{\pi}{4}$ to $\frac{\pi}{4}$ .
Evaluate with New Limits: Evaluate the integral with the new limits. $\newline$ $\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \sec(u) \cdot 2\,du = 2 \cdot \ln|\sec(u) + \tan(u)|$ from $-\frac{\pi}{4}$ to $\frac{\pi}{4}$ .
Calculate Definite Integral: Calculate the definite integral. $\newline$ $2 \times [\ln|\sec(\frac{\pi}{4}) + \tan(\frac{\pi}{4})| - \ln|\sec(-\frac{\pi}{4}) + \tan(-\frac{\pi}{4})|]$ .
Simplify Using Trig Functions: Simplify the expression using the fact that $\sec(\frac{\pi}{4}) = \sqrt{2}$ and $\tan(\frac{\pi}{4}) = 1$ (and similarly for $-\frac{\pi}{4}$ ). $\newline$ $2 \cdot [\ln(\sqrt{2} + 1) - \ln(\sqrt{2} - 1)]$ .
Combine Logarithmic Terms: Use the properties of logarithms to combine the terms. $2 \times \ln\left[\frac{(\sqrt{2} + 1)}{(\sqrt{2} - 1)}\right].$
Rationalize Denominator: Rationalize the denominator of the argument of the logarithm. $\newline$ $2 \cdot \ln\left(\frac{(\sqrt{2} + 1)(\sqrt{2} + 1)}{(\sqrt{2} - 1)(\sqrt{2} + 1)}\right) = 2 \cdot \ln\left(\frac{2 + 2\sqrt{2} + 1}{2 - 1}\right) = 2 \cdot \ln(3 + 2\sqrt{2})$ .
Multiply by Constant Factor: Multiply the result by the constant factor $(\frac{k \lambda}{4R})$ . $\frac{k \lambda}{4R} \times 2 \times \ln(3 + 2\sqrt{2}) = \frac{k \lambda}{2R} \times \ln(3 + 2\sqrt{2})$ .