Full solution
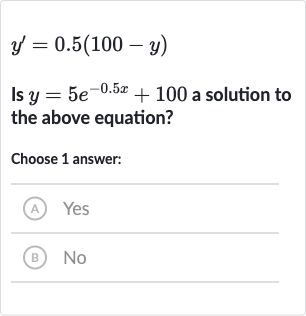
Q. Is a solution to the above equation?Choose answer:(A) Yes(B) No
- Given Differential Equation: Given the differential equation , we need to verify if the function is a solution to this equation.
- Differentiation of : To verify if is a solution, we need to differentiate this function with respect to and check if the derivative matches the right-hand side of the given differential equation.
- Substitute into Equation: Differentiate with respect to using the chain rule for the exponential function.
- Simplify Expression: Now, we substitute into the right-hand side of the given differential equation to see if it matches the derivative we found.Right-hand side of the differential equation:
- Compare Derivative: Simplify the right-hand side expression.
- Compare Derivative: Simplify the right-hand side expression. Compare the derivative with the simplified right-hand side of the differential equation.We found and the right-hand side is also .Since both expressions are equal, is indeed a solution to the differential equation .
More problems from Euler's method
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help