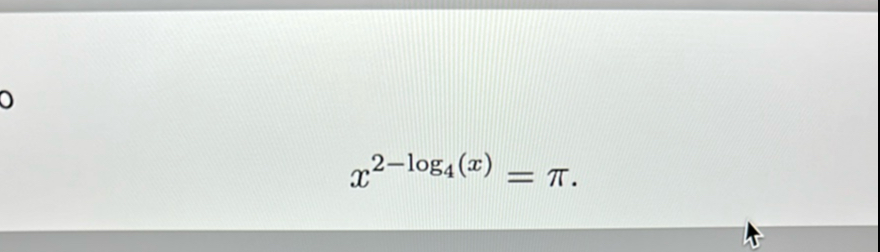x^(2-log_(4)(x))=pi.

Question

Bytelearn · Accepted Answer

Identify Equation and Base: Identify the given equation and the base of the logarithm. The equation is x^(2-log_(4)(x))=pi, and the base of the logarithm is 4.Rewrite Logarithmic Term: Rewrite the logarithmic term using the property of exponents: a^(log_a(b)) = b. Here, we can write x^(log_4(x)) as 4 because 4 is the base of the logarithm.Combine Exponents: Apply the property of exponents to combine the terms with the same base. x^(2) * x^(-log_4(x)) = x^(2 - log_4(x)).Substitute Rewritten Term: Substitute the rewritten logarithmic term back into the equation. x^(2) * 4^(-1) = pi.Recognize Reciprocal: Recognize that 4^(-1) is the reciprocal of 4, which is 1/4. x^(2) * (1/4) = pi.Isolate x^2: Multiply both sides of the equation by 4 to isolate x^(2) on one side. 4 * (x^(2) * (1/4)) = 4 * pi.Take Square Root: Simplify the equation by canceling out the 1/4 on the left side. x^(2) = 4 * pi.Calculate Square Root: Take the square root of both sides to solve for x. x = sqrt(4 * pi).Simplify Square Root: Calculate the square root of 4 * pi. x = sqrt(4) * sqrt(pi).Rewrite Using Exponents: Simplify the square root of 4, which is 2. x = 2 * sqrt(pi).Change of Base Formula: Rewrite the equation using the property of exponents: x^(a-b) = x^a / x^b. x^(2-log_(4)(x)) = x^2 / x^(log_(4)(x)).Simplify Expression: Recognize that x^(log_(4)(x)) can be rewritten using the change of base formula for logarithms: log_(4)(x) = log(x) / log(4). x^(2-log_(4)(x)) = x^2 / (4^(log_(4)(x))).Cancel Out x: Simplify the expression using the property a^(log_a(b)) = b. x^(2-log_(4)(x)) = x^2 / x.Set Equal to pi: Simplify the right side of the equation by canceling out one x. x^(2-log_(4)(x)) = x.Set the simplified expression equal to pi. x = pi.

$x^{2-\log _{4}(x)}=\pi$ .

Full solution

More problems from Evaluate rational exponents

Related topics

x2−log⁡4(x)=π x^{2-\log _{4}(x)}=\pi x2−log4​(x)=π.

$x^{2-\log _{4}(x)}=\pi$ .