AI tutor
Full solution
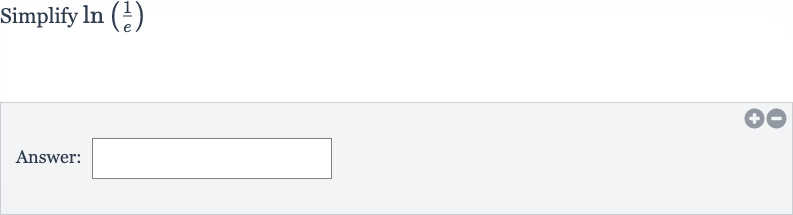
Q. Simplify Answer:
- Identify Properties: Identify the properties of logarithms that can be applied to the problem.The natural logarithm of over , , can be rewritten using the property of logarithms that states .
- Apply Property: Apply the logarithm property to the given expression.
- Simplify Logarithms: Simplify the natural logarithm of and the natural logarithm of . is always because , and is always because . So,
- Calculate Final Value: Calculate the final simplified value.
More problems from Evaluate rational exponents
QuestionGet tutor help
QuestionGet tutor help