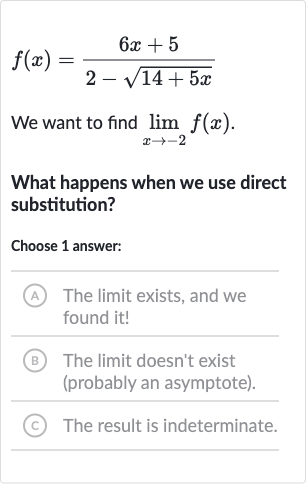
$f(x)=\frac{6 x+5}{2-\sqrt{14+5 x}}$ $\newline$ We want to find $\lim _{x \rightarrow-2} f(x)$ . $\newline$ What happens when we use direct substitution? $\newline$ Choose $1$ answer: $\newline$ (A) The limit exists, and we found it! $\newline$ (B) The limit doesn't exist (probably an asymptote). $\newline$ (C) The result is indeterminate.

Full solution

f(x)=\frac{6 x+5}{2-\sqrt{14+5 x}}

\newline

We want to find

\lim _{x \rightarrow-2} f(x)

\newline

What happens when we use direct substitution?

\newline

Choose

1

answer:

\newline

(A) The limit exists, and we found it!

\newline

(B) The limit doesn't exist (probably an asymptote).

\newline

Substitute $x$ with $-2$ : Substitute $x$ with $-2$ in the function $f(x)$ to see if direct substitution is possible. $\newline$ $f(x) = \frac{6x + 5}{2 - \sqrt{14 + 5x}}$ $\newline$ $f(-2) = \frac{6(-2) + 5}{2 - \sqrt{14 + 5(-2)}}$
Perform calculations after substitution: Perform the calculations inside the function after substitution. $\newline$ $f(-2) = (-12 + 5) / (2 - \sqrt{14 - 10})$ $\newline$ $f(-2) = (-7) / (2 - \sqrt{4})$ $\newline$ $f(-2) = (-7) / (2 - 2)$
Simplify the result of substitution: Simplify the result of the substitution to identify any issues. $\newline$ $f(-2) = \frac{-7}{0}$ $\newline$ We have a division by zero situation, which means the function is undefined at $x = -2$ .
Determine behavior of the limit: Determine the behavior of the limit based on the result of direct substitution. $\newline$ Since we have a division by $0$ , the limit does not exist due to a potential vertical asymptote at $x = -2$ .