Full solution
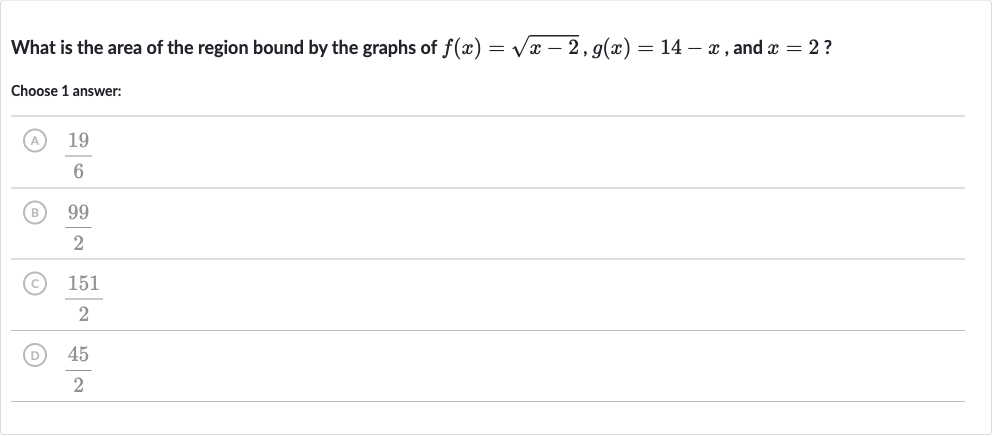
Q. What is the area of the region bound by the graphs of , and ?Choose answer:(A) (B) (C) (D)
- Find Intersection Points: Find the intersection points of and . Set .
- Solve for x: Solve for x: . This simplifies to .
More problems from Operations with rational exponents
QuestionGet tutor help