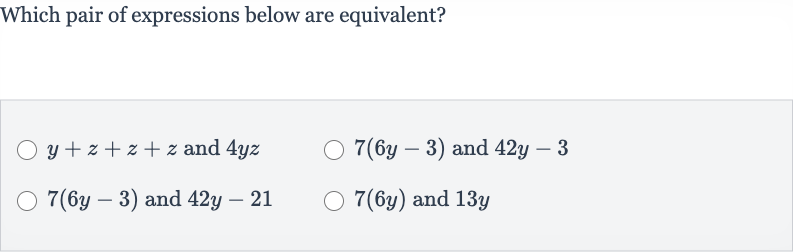Which pair of expressions below are equivalent? y+z+z+z and 4yz 7(6y-3) and 42 y-3 7(6y-3) and 42 y-21 7(6y) and 13 y

Question

Which pair of expressions below are equivalent?  y+z+z+z and  4yz  7(6y-3) and  42 y-3  7(6y-3) and  42 y-21  7(6y) and  13 y

Bytelearn · Accepted Answer

Combine Like Terms: Compare the first pair of expressions y+z+z+z and 4yz. Simplify y+z+z+z by combining like terms. y + z + z + z = y + 3z Check if this is equivalent to 4yz. y + 3z is not equivalent to 4yz because the terms are not similar and cannot be factored or simplified to make the expressions look the same.Distribute and Compare: Compare the second pair of expressions 7(6y-3) and 42y-3. Distribute the 7 in the expression 7(6y-3). 7(6y-3) = 42y - 21 Check if this is equivalent to 42y-3. 42y - 21 is not equivalent to 42y-3 because the constants are different (-21 vs. -3).Check Equivalence: Compare the third pair of expressions 7(6y-3) and 42y-21. Distribute the 7 in the expression 7(6y-3) again. 7(6y-3) = 42y - 21 Check if this is equivalent to 42y-21. 42y - 21 is equivalent to 42y-21 because both expressions are identical after the distribution.Distribute and Compare: Compare the fourth pair of expressions 7(6y) and 13y. Distribute the 7 in the expression 7(6y). 7(6y) = 42y Check if this is equivalent to 13y. 42y is not equivalent to 13y because the coefficients are different (42 vs. 13).

Which pair of expressions below are equivalent? $\newline$ $y+z+z+z$ and $4 y z$ $\newline$ $7(6 y-3)$ and $42 y-3$ $\newline$ $7(6 y-3)$ and $42 y-21$ $\newline$ $7(6 y)$ and $13 y$

Full solution

More problems from Operations with rational exponents

Related topics

Which pair of expressions below are equivalent?\newliney+z+z+z y+z+z+z y+z+z+z and 4yz 4 y z 4yz\newline7(6y−3) 7(6 y-3) 7(6y−3) and 42y−3 42 y-3 42y−3\newline7(6y−3) 7(6 y-3) 7(6y−3) and 42y−21 42 y-21 42y−21\newline7(6y) 7(6 y) 7(6y) and 13y 13 y 13y

Which pair of expressions below are equivalent? $\newline$ $y+z+z+z$ and $4 y z$ $\newline$ $7(6 y-3)$ and $42 y-3$ $\newline$ $7(6 y-3)$ and $42 y-21$ $\newline$ $7(6 y)$ and $13 y$