Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Which expressions are equivalent to
(v^(-1))^((1)/(9)) ?
Choose all answers that apply:
A
(root(9)(v))^(-1)
B
(v^((1)/(9)))^(-1)
C
v^(-(1)/(9))
D None of the above

Which expressions are equivalent to $\left(v^{-1}\right)^{\frac{1}{9}}$ ? $\newline$ Choose all answers that apply: $\newline$ A $(\sqrt[9]{v})^{-1}$ $\newline$ B $\left(v^{\frac{1}{9}}\right)^{-1}$ $\newline$ C $v^{-\frac{1}{9}}$ $\newline$ D None of the above

View step-by-step help

View step-by-step help

Compare linear and exponential growth

Full solution

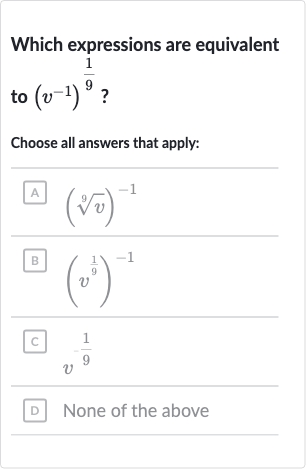
Q. Which expressions are equivalent to

\left(v^{-1}\right)^{\frac{1}{9}}

?

\newline

Choose all answers that apply:

\newline

A

(\sqrt[9]{v})^{-1}

\newline

B

\left(v^{\frac{1}{9}}\right)^{-1}

\newline

C

v^{-\frac{1}{9}}

\newline

D None of the above

Understanding exponent properties: Understand the properties of exponents that will be used to solve the problem. $\newline$ The properties of exponents that are relevant here are: $\newline$ $(a^m)^n = a^{(m*n)}$ - Raising a power to a power means you multiply the exponents. $\newline$ $a^{-n} = \frac{1}{a^n}$ - A negative exponent means that the base is on the opposite side of the fraction line.
Applying exponent property to given expression: Apply the exponent property to the given expression $(v^{-1})^{\frac{1}{9}}$ . Using the property $(a^m)^n = a^{m*n}$ , we get: $(v^{-1})^{\frac{1}{9}} = v^{(-1)*(\frac{1}{9})} = v^{-\frac{1}{9}}$
Comparing the result: Compare the result from Step $2$ with the given choices. $\newline$ We found that $(v^{-1})^{\frac{1}{9}}$ simplifies to $v^{-\frac{1}{9}}$ . $\newline$ Now we need to check which of the given choices are equivalent to this expression.
Evaluating choice A: Evaluate choice A: $(\sqrt[9]{v})^{-1}$ . The expression $(\sqrt[9]{v})^{-1}$ is equivalent to $(v^{1/9})^{-1}$ because the $9$ th root of $v$ is $v$ raised to the $1/9$ power. Using the property $(a^m)^n = a^{m*n}$ , we get: $(v^{1/9})^{-1} = v^{(1/9)*(-1)} = v^{-(1)/(9)}$ This matches the expression we found in Step $2$ .
Evaluating choice B: Evaluate choice B: $(v^{(1/9)})^{-1}$ . This is the same expression we evaluated in Step $4$ , and we have already determined that it is equivalent to $v^{-(1/9)}$ .
Evaluating choice C: Evaluate choice C: $v^{-(1)/(9)}$ . This is exactly the expression we derived in Step $2$ , so it is clearly equivalent to $(v^{-1})^{(1)/(9)}$ .
Evaluating choice D: Evaluate choice D: None of the above. $\newline$ Since we have already found that choices A, B, and C are equivalent to the original expression, choice D is not correct.

More problems from Compare linear and exponential growth

Question

Jill bought a used motorcycle from a seller online for $1,200. The seller will charge her $5 a day to store the motorcycle at his house until she is able to pick it up. You can use a function to describe the total amount of money Jill will owe the seller if she waits

x

days to pick up the motorcycle.

\newline

Write an equation for the function. If it is linear, write it in the form

g(x) = mx + b

. If it is exponential, write it in the form

g(x) = a(b)^x

\newline

g(x) = \underline{\hspace{3em}}

Posted 5 months ago

Question

f(t)=-2t-7

change over the interval from

t=-7

t=-6

\newline

\newline

\left[\text{f(t) decreases by } 2\right]

\newline

\left[\text{f(t) increases by } 2\right]

\newline

\left[\text{f(t) increases by } 200\%\right]

\newline

\left[\text{f(t) decreases by a factor of } 2\right]

Posted 5 months ago

Question

g(t)=9^t

change over the interval from

t=1

t=3

\newline

\newline

\left[\text{g(t) decreases by a factor of } 81\right]

\newline

\left[\text{g(t) increases by a factor of } 81\right]

\newline

\left[\text{g(t) increases by } 18\%\right]

\newline

\left[\text{g(t) decreases by } 9\%\right]

Posted 5 months ago

Question

Both of these functions grow as

x

gets larger and larger. Which function eventually exceeds the other?

\newline

\newline

(A)f(x) = 8x + 3.3

\newline

(B)g(x) = 3.3^x - 5

Posted 6 months ago

Question

Both of these functions grow as

x

gets larger and larger. Which function eventually exceeds the other?

\newline

\newline

(A) \ f(x) = 2x + 9

\newline

(B)\ g(x) = 2^x

Posted 6 months ago

Question

f(x)

g(x)

are differentiable.

\newline

h(x)

h(x)=\frac{g(x)}{f(x)}

\newline

f(8)=1

f'(8)=-6

g(8)=8

g'(8)=-10

h'(8)

\newline

Simplify any fractions.

\newline

h'(8)=

Posted 6 months ago

Question

p(x)

q(x)

are differentiable.

\newline

r(x)

r(x)= \frac{p(x)}{q(x)}

\newline

p(3)= 2

p'(3)= 4

q(3)= 6

q'(3)= 9

r'(3)

\newline

Simplify any fractions.

\newline

r'(3)=

Posted 7 months ago

Question

u(x)

v(x)

are differentiable.

\newline

w(x)

w(x)= \frac{u(x)}{v(x)}

\newline

u(5)= 3

u'(5)= -2

v(5)= 7

v'(5)= 1

w'(5)

\newline

Simplify any fractions.

\newline

w'(5)=

Posted 7 months ago

Question

a(x)

b(x)

are differentiable.

\newline

c(x)

c(x)= \frac{a(x)}{b(x)}

\newline

a(2)= 4

a'(2)= 5

b(2)= 1

b'(2)= -3

c'(2)

\newline

Simplify any fractions.

\newline

c'(2)=

Posted 7 months ago

Question

m(x)

n(x)

are differentiable.

\newline

o(x)

o(x)= \frac{m(x)}{n(x)}

\newline

m(7)= 2

m'(7)= -1

n(7)= 4

n'(7)= 8

o'(7)

\newline

Simplify any fractions.

\newline

o'(7)=

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant