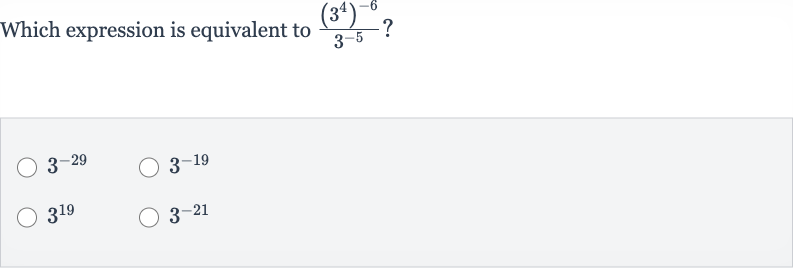AI tutor
Full solution
Q. Which expression is equivalent to
- Simplify numerator: Simplify the numerator . When raising a power to another power, we multiply the exponents.
- Simplify denominator: Simplify the denominator . The denominator is already in its simplest form, so we can leave it as .
- Divide numerator by denominator: Divide the numerator by the denominator.When dividing like bases with exponents, we subtract the exponents.
- Verify final expression: Verify the final expression.The final expression is , which is one of the options given.
More problems from Operations with rational exponents
QuestionGet tutor help
QuestionGet tutor help