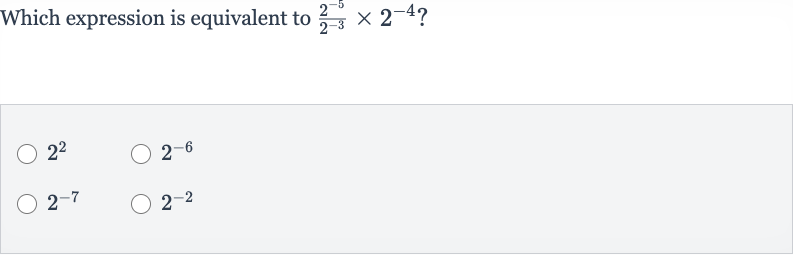AI tutor
Full solution
Q. Which expression is equivalent to ?
- Identify Properties: Identify the properties of exponents that will be used to simplify the expression. When dividing like bases with exponents, subtract the exponents: . When multiplying like bases with exponents, add the exponents: .
- Apply Division Property: Apply the division property to . Subtract the exponents: .So, simplifies to .
- Multiply Result: Now multiply the result, , by using the multiplication property of exponents. Add the exponents: . So, simplifies to .
- Check Final Result: Check the final result to ensure no mathematical errors were made. The properties of exponents have been correctly applied, and the calculations are correct.
More problems from Operations with rational exponents
QuestionGet tutor help
QuestionGet tutor help