What is the area of the region bound by the graphs of $f(x)=\sqrt{x-2}$ , $g(x)=14-x$ , and $x=2$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{19}{6}$ $\newline$ (B) $\frac{99}{2}$ $\newline$ (C) $\frac{151}{2}$ $\newline$ (D) $\frac{45}{2}$

View step-by-step help

Home

Math Problems

Precalculus

Operations with rational exponents

Full solution

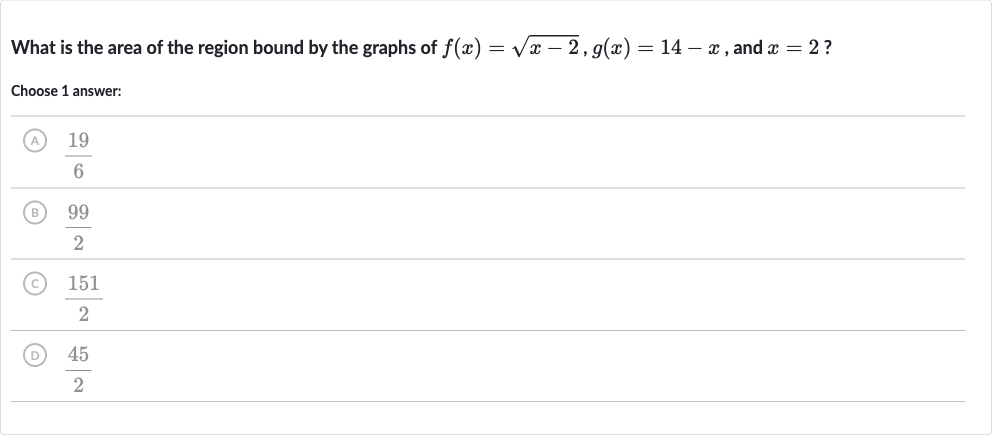
Q. What is the area of the region bound by the graphs of

f(x)=\sqrt{x-2}

g(x)=14-x

, and

x=2

\newline

Choose

1

answer:

\newline

(A)

\frac{19}{6}

\newline

(B)

\frac{99}{2}

\newline

(C)

\frac{151}{2}

\newline

(D)

\frac{45}{2}

Find Intersection Points: First, find the intersection points of $f(x)$ and $g(x)$ to determine the limits of integration. $\newline$ Set $f(x) = g(x)$ : $\sqrt{x-2} = 14-x$ .
Square Both Sides: Square both sides to get rid of the square root: $(\sqrt{x-2})^2 = (14-x)^2.$ This gives us $x-2 = (14-x)^2.$
Expand and Rearrange Equation: Expand the right side: $x-2 = 196 - 28x + x^2$ .
Factor and Solve for $x$ : Rearrange the equation to form a quadratic equation: $x^2 - 29x + 198 = 0$ .
Set Up Integral: Factor the quadratic equation: $(x-11)(x-18) = 0$ .
Calculate Integral: Solve for $x$ : $x = 11$ or $x = 18$ . These are the intersection points, so the limits of integration are from $x=2$ to $x=11$ .
Integrate First Part: Set up the integral to find the area between the curves from $x=2$ to $x=11$ : $\int_{2}^{11} (14-x - \sqrt{x-2}) \, dx$ .
Evaluate First Integral: Calculate the integral: $\int_{2}^{11} (14-x) \, dx - \int_{2}^{11} \sqrt{x-2} \, dx$ .
Integrate Second Part: Integrate the first part: $\int_{2}^{11} (14-x) \, dx = [14x - \frac{x^2}{2}]$ from $2$ to $11$ .
Evaluate Second Integral: Evaluate the first integral at the bounds: $14\cdot 11 - \frac{11^2}{2}$ - $14\cdot 2 - \frac{2^2}{2}$ .
Subtract and Calculate Final Area: Calculate the values: $(154 - 60.5) - (28 - 2)$ .
Subtract and Calculate Final Area: Calculate the values: $154 - 60.5$ - $28 - 2$ .Simplify the result: $93.5 - 26 = 67.5$ .
Subtract and Calculate Final Area: Calculate the values: $(154 - 60.5) - (28 - 2)$ .Simplify the result: $93.5 - 26 = 67.5$ .Integrate the second part: $\int_{2}^{11} \sqrt{x-2} \, dx$ . $Let \, u = x-2, \, then \, du = dx$ and change the limits accordingly.
Subtract and Calculate Final Area: Calculate the values: $(154 - 60.5) - (28 - 2)$ .Simplify the result: $93.5 - 26 = 67.5$ .Integrate the second part: $\int_{2}^{11} \sqrt{x-2} \, dx$ . Let $u = x-2$ , then $du = dx$ and change the limits accordingly.The new limits are from $u=0$ to $u=9$ . Calculate the integral: $\int_{0}^{9} \sqrt{u} \, du$ .
Subtract and Calculate Final Area: Calculate the values: $(154 - 60.5) - (28 - 2)$ .Simplify the result: $93.5 - 26 = 67.5$ .Integrate the second part: $\int_{2}^{11} \sqrt{x-2} \, dx$ . Let $u = x-2$ , then $du = dx$ and change the limits accordingly.The new limits are from $u=0$ to $u=9$ . Calculate the integral: $\int_{0}^{9} \sqrt{u} \, du$ .Integrate: $\int_{0}^{9} \sqrt{u} \, du = \left[\frac{2}{3} * u^{\frac{3}{2}}\right]$ from $0$ to $93.5 - 26 = 67.5$ $0$ .
Subtract and Calculate Final Area: Calculate the values: $154 - 60.5$ - $28 - 2$ . Simplify the result: $93.5 - 26 = 67.5$ . Integrate the second part: $extstyle\int_{2}^{11} \sqrt{x-2} \, dx$ . Let $u = x-2$ , then $du = dx$ and change the limits accordingly. The new limits are from $u=0$ to $u=9$ . Calculate the integral: $extstyle\int_{0}^{9} \sqrt{u} \, du$ . Integrate: $extstyle\int_{0}^{9} \sqrt{u} \, du = \left[\frac{2}{3} * u^{\frac{3}{2}}\right]_{0}^{9}$ . Evaluate the integral at the bounds: $28 - 2$ $0$ .
Subtract and Calculate Final Area: Calculate the values: $154 - 60.5$ - $28 - 2$ . Simplify the result: $93.5 - 26 = 67.5$ . Integrate the second part: $extstyle\int_{2}^{11} \sqrt{x-2} \, dx$ . Let $u = x-2$ , then $du = dx$ and change the limits accordingly. The new limits are from $u=0$ to $u=9$ . Calculate the integral: $extstyle\int_{0}^{9} \sqrt{u} \, du$ . Integrate: $extstyle\int_{0}^{9} \sqrt{u} \, du = \left[\frac{2}{3} * u^{\frac{3}{2}}\right]$ from $28 - 2$ $0$ to $28 - 2$ $1$ . Evaluate the integral at the bounds: $28 - 2$ $2$ . Calculate the values: $28 - 2$ $3$ .
Subtract and Calculate Final Area: Calculate the values: $(154 - 60.5) - (28 - 2)$ .Simplify the result: $93.5 - 26 = 67.5$ .Integrate the second part: $\int_{2}^{11} \sqrt{x-2} \, dx$ . Let $u = x-2$ , then $du = dx$ and change the limits accordingly.The new limits are from $u=0$ to $u=9$ . Calculate the integral: $\int_{0}^{9} \sqrt{u} \, du$ .Integrate: $\int_{0}^{9} \sqrt{u} \, du = \left[\frac{2}{3} * u^{\frac{3}{2}}\right]$ from $0$ to $93.5 - 26 = 67.5$ $0$ .Evaluate the integral at the bounds: $93.5 - 26 = 67.5$ $1$ .Calculate the values: $93.5 - 26 = 67.5$ $2$ .Simplify the result: $93.5 - 26 = 67.5$ $3$ .
Subtract and Calculate Final Area: Calculate the values: $(154 - 60.5) - (28 - 2)$ . Simplify the result: $93.5 - 26 = 67.5$ . Integrate the second part: $\int_{2}^{11} \sqrt{x-2} \, dx$ . Let $u = x-2$ , then $du = dx$ and change the limits accordingly. The new limits are from $u=0$ to $u=9$ . Calculate the integral: $\int_{0}^{9} \sqrt{u} \, du$ . Integrate: $\int_{0}^{9} \sqrt{u} \, du = \left[\frac{2}{3} * u^{\frac{3}{2}}\right]$ from $0$ to $93.5 - 26 = 67.5$ $0$ . Evaluate the integral at the bounds: $93.5 - 26 = 67.5$ $1$ . Calculate the values: $93.5 - 26 = 67.5$ $2$ . Simplify the result: $93.5 - 26 = 67.5$ $3$ . Subtract the second integral from the first to find the total area: $93.5 - 26 = 67.5$ $4$ .
Subtract and Calculate Final Area: Calculate the values: $(154 - 60.5) - (28 - 2)$ .Simplify the result: $93.5 - 26 = 67.5$ .Integrate the second part: $\int_{2}^{11} \sqrt{x-2} \, dx$ . Let $u = x-2$ , then $du = dx$ and change the limits accordingly.The new limits are from $u=0$ to $u=9$ . Calculate the integral: $\int_{0}^{9} \sqrt{u} \, du$ .Integrate: $\int_{0}^{9} \sqrt{u} \, du = \left[\frac{2}{3} * u^{\frac{3}{2}}\right]$ from $0$ to $93.5 - 26 = 67.5$ $0$ .Evaluate the integral at the bounds: $93.5 - 26 = 67.5$ $1$ .Calculate the values: $93.5 - 26 = 67.5$ $2$ .Simplify the result: $93.5 - 26 = 67.5$ $3$ .Subtract the second integral from the first to find the total area: $93.5 - 26 = 67.5$ $4$ .Calculate the final area: $93.5 - 26 = 67.5$ $5$ .