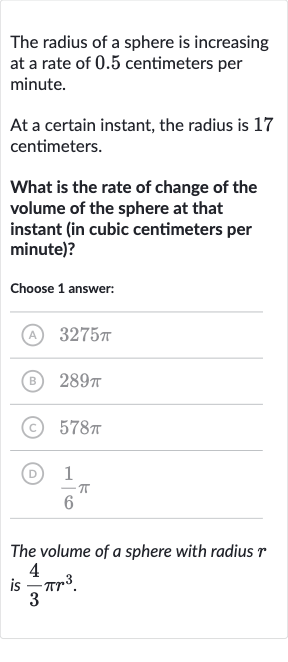
The radius of a sphere is increasing at a rate of $0$ . $5$ centimeters per minute. $\newline$ At a certain instant, the radius is $17$ centimeters. $\newline$ What is the rate of change of the volume of the sphere at that instant (in cubic centimeters per minute)? $\newline$ Choose $1$ answer: $\newline$ (A) $3275 \pi$ $\newline$ (B) $289 \pi$ $\newline$ (C) $578 \pi$ $\newline$ (D) $\frac{1}{6} \pi$ $\newline$ The volume of a sphere with radius $r$ is $\frac{4}{3} \pi r^{3}$ .

Full solution

Q. The radius of a sphere is increasing at a rate of

0

5

centimeters per minute.

\newline

At a certain instant, the radius is

17

centimeters.

\newline

What is the rate of change of the volume of the sphere at that instant (in cubic centimeters per minute)?

\newline

Choose

1

answer:

\newline

(A)

3275 \pi

\newline

(B)

289 \pi

\newline

(C)

578 \pi

\newline

(D)

\frac{1}{6} \pi

\newline

The volume of a sphere with radius

r

\frac{4}{3} \pi r^{3}

Volume Formula Derivation: The formula for the volume of a sphere is $V = \frac{4}{3}\pi r^3$ . We need to find $\frac{dV}{dt}$ , the rate of change of volume with respect to time.
Differentiation with Chain Rule: First, differentiate $V = \frac{4}{3}\pi r^3$ with respect to time $t$ to get $\frac{dV}{dt}$ . Using the chain rule, $\frac{dV}{dt} = 4\pi r^2 \cdot \frac{dr}{dt}$ .
Substitute Values: We know $\frac{dr}{dt} = 0.5\,\text{cm/min}$ (the rate at which the radius is increasing) and $r = 17\,\text{cm}$ (the radius at the instant we're interested in).
Calculate $\frac{dV}{dt}$ : Substitute $r = 17$ cm and $\frac{dr}{dt} = 0.5$ cm/min into $\frac{dV}{dt} = 4\pi r^2 \cdot \frac{dr}{dt}$ to find the rate of change of volume.
Calculate $\frac{dV}{dt}$ : Substitute $r = 17 \, \text{cm}$ and $\frac{dr}{dt} = 0.5 \, \text{cm/min}$ into $\frac{dV}{dt} = 4\pi r^2 \cdot \frac{dr}{dt}$ to find the rate of change of volume.$\frac{dV}{dt} = $4$\pi($17$)^$2$ \cdot $0$.$5$ = $4$\pi($289$) \cdot $0$.$5$ = $578$\pi \, \text{cubic centimeters per minute}.