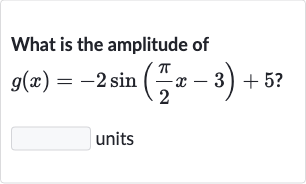Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

What is the amplitude of g(x)=-2sin((pi)/(2)x-3)+5? units

What is the amplitude of\newlineg(x)=−2sin⁡(π2x−3)+5? g(x)=-2 \sin \left(\frac{\pi}{2} x-3\right)+5 ? \newlineunits

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Domain and range of quadratic functions: equationsright chevron icon

Full solution

Q. What is the amplitude of\newlineg(x)=−2sin⁡(π2x−3)+5? g(x)=-2 \sin \left(\frac{\pi}{2} x-3\right)+5 ? \newlineunits
  1. Identify standard form: Identify the standard form of a sine function.\newlineThe standard form of a sine function is y=Asin⁡(Bx−C)+Dy = A\sin(Bx - C) + D, where AA is the amplitude, BB affects the period, CC is the phase shift, and DD is the vertical shift.
  2. Compare given function: Compare the given function to the standard form.\newlineThe given function is g(x)=−2sin⁡(π2x−3)+5g(x) = -2\sin\left(\frac{\pi}{2}x - 3\right) + 5. Here, A=−2A = -2, B=π2B = \frac{\pi}{2}, C=3C = 3, and D=5D = 5.
  3. Determine amplitude: Determine the amplitude.\newlineThe amplitude is the absolute value of AA. In this case, A=−2A = -2, so the amplitude is ∣A∣=∣−2∣=2|A| = |-2| = 2.
  4. Check for errors: Check for any mathematical errors.\newlineThere are no mathematical errors in the previous steps.

More problems from Domain and range of quadratic functions: equations

Question
The function h h is defined over the real numbers. This table gives a few values of h h .\newline\begin{tabular}{lllll}\newlinex x & −6-6.11 & −6-6.0101 & −6-6.001001 & −5-5.99 \\\newline\hlineh(x) h(x) & −0-0.2525 & −0-0.7474 & −0-0.9898 & −1-1.00\newline\end{tabular}\newlineWhat is a reasonable estimate for lim⁡x→−6h(x) \lim _{x \rightarrow-6} h(x) ?\newlineChoose 11 answer:\newline(A) −6-6\newline(B) −2-2\newline(C) −1-1\newline(D) The limit doesn't exist
Get tutor helpright-arrow

Posted 4 months ago

Question
What is the amplitude of y=5sin⁡(4x−2)−3 y=5 \sin (4 x-2)-3 ?\newlineunits
Get tutor helpright-arrow

Posted 3 months ago

Question
What is the amplitude of y=−3cos⁡(πx+2)−6? y=-3 \cos (\pi x+2)-6 ? \newlineunits
Get tutor helpright-arrow

Posted 3 months ago

Question
What is the amplitude of y=3sin⁡(2x−1)+4 y=3 \sin (2 x-1)+4 ?\newlineunits
Get tutor helpright-arrow

Posted 3 months ago

Question
What is the period of the function h(x)=−3cos⁡(πx+2)−6? h(x)=-3 \cos (\pi x+2)-6 ? \newlineGive an exact value.\newlineunits
Get tutor helpright-arrow

Posted 3 months ago

Question
What is the period of the function\newlineh(x)=5sin⁡(4x−2)−3 ?  h(x)=5 \sin (4 x-2)-3 \text { ? } \newlineGive an exact value.\newlineunits
Get tutor helpright-arrow

Posted 3 months ago

Question
What is the period of the function g(x)=2cos⁡(7x+5)+1? g(x)=2 \cos (7 x+5)+1 ? \newlineGive an exact value.\newlineunits
Get tutor helpright-arrow

Posted 3 months ago

Question
What is the period of the function f(x)=3sin⁡(2x−1)+4 f(x)=3 \sin (2 x-1)+4 ?\newlineGive an exact value.\newlineunits
Get tutor helpright-arrow

Posted 3 months ago

Question
What is the period of the function f(x)=−4cos⁡(5x−9)−7 f(x)=-4 \cos (5 x-9)-7 ?\newlineGive an exact value.\newlineunits
Get tutor helpright-arrow

Posted 3 months ago

Question
warming. As of 20202020 , China is the largest emitter of carbon dioxide gas in the world, with 1010,668668 million metric tons. The US is the secondlargest emituer of CO2 \mathrm{CO}_{2} with 44,713713 million metric tons. India is the thirdlargest emitter, with 22,442442 million metric tons of total carbon dioxide emissions produced. Russia is the fourth-largest emitting 11,577577 million metrictons.\newlineNow, complete the following on A44-sized sheets-\newlinea. Draw a bar graph to represent the data given, taking 1 cm−1000 1 \mathrm{~cm}-1000 metric tons.
Get tutor helpright-arrow

Posted 9 hours ago

View all (6)