Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

The positive numbers
x and
a-x have a sum of
a. What is
x in terms of
a if the product
x*(a-x) is a maximum?
Choose 1 answer:
(A)
(a)/(2)
(B)
sqrt((a)/(2))
(C)
sqrta
(D)
a
E There is no
x that would produce a maximum product

The positive numbers $x$ and $a-x$ have a sum of $a$ . What is $x$ in terms of $a$ if the product $x \cdot(a-x)$ is a maximum? $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{a}{2}$ $\newline$ (B) $\sqrt{\frac{a}{2}}$ $\newline$ (C) $\sqrt{a}$ $\newline$ (D) $a$ $\newline$ (E) There is no $x$ that would produce a maximum product

View step-by-step help

View step-by-step help

Simplify radical expressions with variables II

Full solution

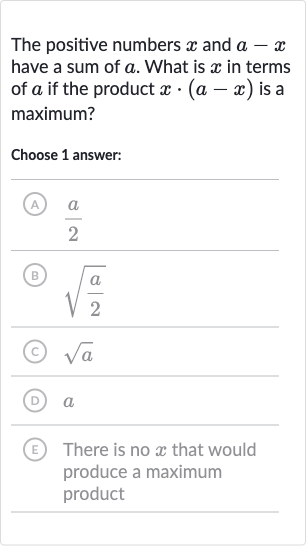
Q. The positive numbers

x

and

a-x

have a sum of

a

. What is

x

in terms of

a

if the product

x \cdot(a-x)

is a maximum?

\newline

Choose

1

answer:

\newline

(A)

\frac{a}{2}

\newline

(B)

\sqrt{\frac{a}{2}}

\newline

(C)

\sqrt{a}

\newline

(D)

a

\newline

(E) There is no

x

that would produce a maximum product

Equation Simplification: We know that $x + (a - x) = a$ . This simplifies to $x + a - x = a$ , which means $x$ cancels out and we're left with $a = a$ , which is true but doesn't help us find $x$ .
Maximizing Product: To maximize the product $x(a-x)$ , we can use the fact that for a fixed sum, the product of two numbers is maximized when the numbers are equal. So, we set $x = a - x$ .
Solving for x: Solving for x gives us $x = a - x$ , which simplifies to $2x = a$ .
Isolating $x$ : Divide both sides by $2$ to isolate $x$ , we get $x = \frac{a}{2}$ .

More problems from Simplify radical expressions with variables II

Question

Order the expressions from least to greatest.

\newline

11^{1} \quad8^{2}-60 \quad 2^{2} \times 5

Posted 4 months ago

Question

Order the expressions from least to greatest.

\newline

2^{3}-2^{1} \quad 2^{1}+3^{1} \quad 3^{2}

Posted 4 months ago

Question

y=\sqrt{e^{x}}

\newline

\frac{d y}{d x}

\newline

1

\newline

\frac{\sqrt{e^{x}}}{2}

\newline

\sqrt{e^{x}}

\newline

x \sqrt{e^{x-1}}

\newline

\frac{1}{2 \sqrt{e^{x}}}

Posted 3 months ago

Question

What is the area of the region between the graphs of

f(x)=-x^{2}+2 x+12

g(x)=x^{2}-12

x=-3

x=4

\newline

1

\newline

7

\newline

\frac{343}{3}

\newline

\frac{83}{3}

\newline

\frac{52}{3} \sqrt{13}-1-32 \sqrt{3}

Posted 3 months ago

Question

What is the average value of

\frac{1}{x}

on the interval

4 \leq x \leq 8

\newline

1

\newline

\frac{3}{16}

\newline

\frac{1}{16}

\newline

\frac{\ln (32)}{4}

\newline

\frac{\ln (2)}{4}

Posted 3 months ago

Question

4

6

\newline

K

\newline

For the data given below, answer parts (a) through (f).

\newline

\begin{array}{cc}

\newline

x & y (\newline\)

-19

102

-16

122

-14

120

-13

132

-9

142

(\newline\)\end{array}

\newline

(a) Draw a scatter plot.

\newline

Choose the correct graph below.

\newline

\newline

\newline

\newline

\newline

(b) Find the equation of the line containing the first and the last data points.

\newline

y=4x+178

\newline

(Type an equation. Type your answer in slope-intercept form. Use integers or fractions for any numbers in the equation.)

\newline

(c) Graph the line found in part (b) on the scatter plot.

\newline

Choose the correct graph below.

\newline

\newline

\newline

\newline

(d) Use a graphing utility to find the line of best fit.

\newline

y=\square x+\square

\newline

(Type integers or decimals rounded to four decimal places as needed)

Posted 3 months ago

Question

noot: Additional Practice (LMS graded)

\newline

2

\newline

e surface area of a paper cup is defined by the function

\newline

s(h)=6\pi\sqrt{16+h^{2}}

\newline

h

is the height of the cup. What is the domain and range of

\newline

s(h)

\newline

Describe the domain. Select the correct choice below and, if necessary, fill in the answer box within your choice.

\newline

A. The domain is

\newline

\{h\mid h>-\}

\newline

(Type an inequality or a compound inequality. Simplify your answer. Type an exact answer, using

\newline

\pi

\newline

B. The domain is all real numbers.

Posted 3 months ago

Question

Determine the coefficient and degree of the monomial.

\newline

-7x^{2}y^{5}

\newline

The coefficient of the monomial is

\newline

\square

\newline

The degree of the monomial is

\newline

\square

Posted 3 months ago

Question

\dfrac{a^2a^{-5}}{a^{-3}a^0}\cdot\left(\dfrac{a^2}{a^3}\right)^{-4}=a^x

Posted 3 months ago

Question

\frac{x}{3} + \frac{4x}{5} = \frac{1}{3}

Posted 3 months ago