Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

What is the average value of (1)/(x) on the interval 4 <= x <= 8 ? Choose 1 answer: (A) (3)/(16) (B) (1)/(16) (C) (ln(32))/(4) (D) (ln(2))/(4)

What is the average value of 1x \frac{1}{x} on the interval 4≤x≤8 4 \leq x \leq 8 ?\newlineChoose 11 answer:\newline(A) 316 \frac{3}{16} \newline(B) 116 \frac{1}{16} \newline(C) ln⁡(32)4 \frac{\ln (32)}{4} \newline(D) ln⁡(2)4 \frac{\ln (2)}{4}

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Roots of rational numbersright chevron icon

Full solution

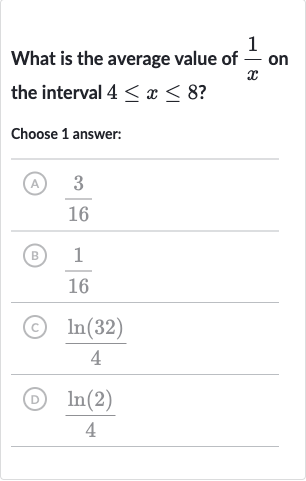
Q. What is the average value of 1x \frac{1}{x} on the interval 4≤x≤8 4 \leq x \leq 8 ?\newlineChoose 11 answer:\newline(A) 316 \frac{3}{16} \newline(B) 116 \frac{1}{16} \newline(C) ln⁡(32)4 \frac{\ln (32)}{4} \newline(D) ln⁡(2)4 \frac{\ln (2)}{4}
  1. Define Average Value Formula: To find the average value of a function f(x)f(x) on the interval [a,b][a, b], we use the formula:\newlineAverage value = 1(b−a)⋅∫abf(x) dx\frac{1}{(b-a)} \cdot \int_{a}^{b} f(x) \, dx\newlineHere, f(x)=1xf(x) = \frac{1}{x}, a=4a = 4, and b=8b = 8.
  2. Calculate Integral of 1/x1/x: First, we calculate the integral of 1/x1/x from 44 to 88. The integral of 1/x1/x dx is ln⁡∣x∣\ln|x|, so we evaluate ln⁡∣x∣\ln|x| from 44 to 88. ∫481xdx=ln⁡∣8∣−ln⁡∣4∣\int_{4}^{8} \frac{1}{x} dx = \ln|8| - \ln|4|
  3. Substitute Values into ln⁡∣x∣\ln|x|: Now we substitute the values of x=8x = 8 and x=4x = 4 into ln⁡∣x∣\ln|x|.ln⁡∣8∣−ln⁡∣4∣=ln⁡(8)−ln⁡(4)\ln|8| - \ln|4| = \ln(8) - \ln(4)
  4. Simplify Logarithmic Expression: We use the properties of logarithms to simplify the expression. ln⁡(8)−ln⁡(4)=ln⁡(84)=ln⁡(2)\ln(8) - \ln(4) = \ln\left(\frac{8}{4}\right) = \ln(2)
  5. Calculate Average Value: Now we calculate the average value using the formula.\newlineAverage value = (1/(8−4))×ln⁡(2)(1/(8-4)) \times \ln(2)\newlineAverage value = (1/4)×ln⁡(2)(1/4) \times \ln(2)
  6. Final Result: The average value of (1)/(x)(1)/(x) on the interval [4,8][4, 8] is (ln⁡(2))/(4)(\ln(2))/(4). This corresponds to answer choice (D)(D).

More problems from Roots of rational numbers

Question
Order the expressions from least to greatest.\newline11182−6022×5 11^{1} \quad8^{2}-60 \quad 2^{2} \times 5
Get tutor helpright-arrow

Posted 8 months ago

Question
Order the expressions from least to greatest.\newline23−2121+3132 2^{3}-2^{1} \quad 2^{1}+3^{1} \quad 3^{2}
Get tutor helpright-arrow

Posted 8 months ago

Question
Let y=ex y=\sqrt{e^{x}} .\newlineFind dydx \frac{d y}{d x} .\newlineChoose 11 answer:\newline(A) ex2 \frac{\sqrt{e^{x}}}{2} \newline(B) ex \sqrt{e^{x}} \newline(C) xex−1 x \sqrt{e^{x-1}} \newline(D) 12ex \frac{1}{2 \sqrt{e^{x}}}
Get tutor helpright-arrow

Posted 7 months ago

Question
What is the area of the region between the graphs of f(x)=−x2+2x+12 f(x)=-x^{2}+2 x+12 and g(x)=x2−12 g(x)=x^{2}-12 from x=−3 x=-3 to x=4 x=4 ?\newlineChoose 11 answer:\newline(A) 77\newline(B) 3433 \frac{343}{3} \newline(C) 833 \frac{83}{3} \newline(D) 52313−1−323 \frac{52}{3} \sqrt{13}-1-32 \sqrt{3}
Get tutor helpright-arrow

Posted 7 months ago

Question
Part 44 of 66\newlineKK\newlineFor the data given below, answer parts (a) through (f).\newline\begin{array}{cc}\newlinex & y (\newline\)−19-19 & 102102 (\newline\)−16-16 & 122122 (\newline\)−14-14 & 120120 (\newline\)−13-13 & 132132 (\newline\)−9-9 & 142142 (\newline\)\end{array}\newline(a) Draw a scatter plot.\newlineChoose the correct graph below.\newlineA.\newlineB.\newlineC.\newlineD.\newline(b) Find the equation of the line containing the first and the last data points.\newliney=4x+178y=4x+178\newline(Type an equation. Type your answer in slope-intercept form. Use integers or fractions for any numbers in the equation.)\newline(c) Graph the line found in part (b) on the scatter plot.\newlineChoose the correct graph below.\newlineA.\newlineB\newlineC.\newline(d) Use a graphing utility to find the line of best fit.\newliney=□x+□y=\square x+\square\newline(Type integers or decimals rounded to four decimal places as needed)
Get tutor helpright-arrow

Posted 7 months ago

Question
noot: Additional Practice (LMS graded)\newlineof 22\newlinee surface area of a paper cup is defined by the function \newlines(h)=6π16+h2s(h)=6\pi\sqrt{16+h^{2}}, where \newlinehh is the height of the cup. What is the domain and range of \newlines(h)s(h) ?\newlineDescribe the domain. Select the correct choice below and, if necessary, fill in the answer box within your choice.\newlineA. The domain is \newline{h∣h>−}\{h\mid h>-\}.\newline(Type an inequality or a compound inequality. Simplify your answer. Type an exact answer, using \newlineπ\pi as needed.)\newlineB. The domain is all real numbers.
Get tutor helpright-arrow

Posted 7 months ago

Question
Determine the coefficient and degree of the monomial.\newline−7x2y5-7x^{2}y^{5}\newlineThe coefficient of the monomial is \newline□\square.\newlineThe degree of the monomial is \newline□\square.
Get tutor helpright-arrow

Posted 6 months ago

Question
x3+4x5=13\frac{x}{3} + \frac{4x}{5} = \frac{1}{3}
Get tutor helpright-arrow

Posted 6 months ago

Question
Consider the following polynomial.\newlineq(x)=4x2−3x+12q(x)=4x^{2}-3x+12\newlineStep 22 of 22: Describe the behavior of the graph of q(x)q(x) as x→±∞x \rightarrow \pm\infty.\newlineq(x)→□q(x)\rightarrow \square as x→−∞x \rightarrow -\infty
Get tutor helpright-arrow

Posted 6 months ago

Question
With a mass of 112.67112.67 grams, the Star of India is one of the largest star sapphires in the world. The density of a star sapphire is approximately 4.04.0 grams per cubic centimeter. \newlineWhich of the following best approximates the volume, in cubic centimeters, of the Star of India?
Get tutor helpright-arrow

Posted 23 hours ago

View all (12)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant