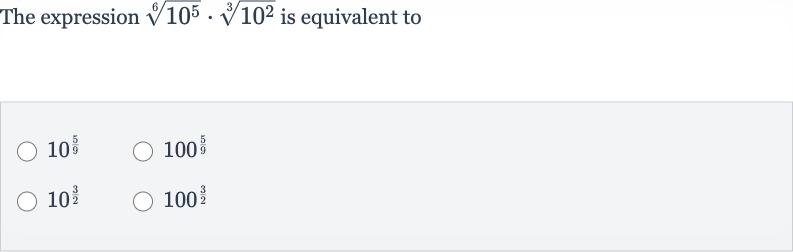AI tutor
Full solution
Q. The expression is equivalent to
- Rewrite Roots as Exponents: Rewrite the roots as fractional exponents.The root of can be written as , and the cube root of can be written as .
- Apply Power of Power Rule: Apply the power of a power rule.When you have a power to a power, you multiply the exponents. So, becomes , and becomes .
- Multiply Expressions: Multiply the two expressions.Now we have . Since the bases are the same, we can add the exponents.
- Add Exponents: Add the exponents.We add the fractions and . To add these fractions, we need a common denominator, which is . So we convert to and then add: .
- Simplify Exponent: Simplify the exponent.The fraction can be simplified to . So now we have .
- Check for Further Simplification: Determine if the expression can be further simplified. is already in its simplest form, and it matches one of the answer choices.
More problems from Operations with rational exponents
QuestionGet tutor help
QuestionGet tutor help