The derivative of the function $f$ is defined by $f^{\prime}(x)=x^{2} \cos (x-3)$ . If $f(-2)=-4$ , then use a calculator to find the value of $f(6)$ to the nearest thousandth. $\newline$ Answer:

View step-by-step help

Home

Math Problems

Precalculus

Find roots using a calculator

Full solution

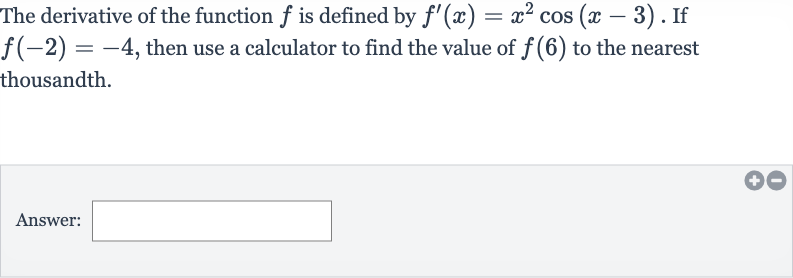
Q. The derivative of the function

f

is defined by

f^{\prime}(x)=x^{2} \cos (x-3)

. If

f(-2)=-4

, then use a calculator to find the value of

f(6)

to the nearest thousandth.

\newline

Answer:

Integrate $f'(x)$ : To find the value of $f(6)$ , we need to integrate the derivative $f'(x)$ to get the original function $f(x)$ . We will then use the initial condition $f(-2) = -4$ to find the constant of integration.
Apply integration by parts: Integrate $f'(x) = x^2\cos(x-3)$ with respect to $x$ . This requires integration by parts or a special technique since it is a product of a polynomial and a trigonometric function.
Simplify and integrate: Let $u = x^2$ , which means $du = 2x\,dx$ . Let $dv = \cos(x-3)\,dx$ , which means $v = \int\cos(x-3)\,dx = \sin(x-3)$ . Now we can apply integration by parts: $\int u\,dv = uv - \int v\,du$ .
Use initial condition: Using integration by parts, we get $f(x) = x^2\sin(x-3) - \int 2x\sin(x-3)\,dx$ . The second integral also requires integration by parts.
Calculate trigonometric values: Let $u = 2x$ , which means $du = 2dx$ . Let $dv = \sin(x-3)dx$ , which means $v = -\cos(x-3)$ . Apply integration by parts again: $\int u dv = uv - \int v du$ .
Find constant of integration: We get $f(x) = x^2\sin(x-3) - (2x(-\cos(x-3)) - \int -2\cos(x-3)\,dx)$ . Simplify and integrate the remaining term.
Find $f(6)$ : Simplifying, we have $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ . The last integral is straightforward: $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ .
Find $f(6)$ : Simplifying, we have $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ . The last integral is straightforward: $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ .Putting it all together, we have $f(x) = x^2\sin(x-3) + 2x\cos(x-3) + 2\sin(x-3) + C$ , where $C$ is the constant of integration.
Find $f(6)$ : Simplifying, we have $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ . The last integral is straightforward: $\int -2\cos(x-3)dx = -2\sin(x-3)$ .Putting it all together, we have $f(x) = x^2\sin(x-3) + 2x\cos(x-3) + 2\sin(x-3) + C$ , where $C$ is the constant of integration.Now we use the initial condition $f(-2) = -4$ to solve for $C$ . Plug in $x = -2$ into the equation: $-4 = (-2)^2\sin(-2-3) + 2(-2)\cos(-2-3) + 2\sin(-2-3) + C$ .
Find $f(6)$ : Simplifying, we have $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ . The last integral is straightforward: $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ . Putting it all together, we have $f(x) = x^2\sin(x-3) + 2x\cos(x-3) + 2\sin(x-3) + C$ , where $C$ is the constant of integration. Now we use the initial condition $f(-2) = -4$ to solve for $C$ . Plug in $x = -2$ into the equation: $-4 = (-2)^2\sin(-2-3) + 2(-2)\cos(-2-3) + 2\sin(-2-3) + C$ . Calculate the trigonometric values and simplify: $-4 = 4\sin(-5) - 4\cos(-5) + 2\sin(-5) + C$ . Use a calculator to find the values of $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $0$ and $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $1$ .
Find $f(6)$ : Simplifying, we have $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ . The last integral is straightforward: $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ . Putting it all together, we have $f(x) = x^2\sin(x-3) + 2x\cos(x-3) + 2\sin(x-3) + C$ , where $C$ is the constant of integration. Now we use the initial condition $f(-2) = -4$ to solve for $C$ . Plug in $x = -2$ into the equation: $-4 = (-2)^2\sin(-2-3) + 2(-2)\cos(-2-3) + 2\sin(-2-3) + C$ . Calculate the trigonometric values and simplify: $-4 = 4\sin(-5) - 4\cos(-5) + 2\sin(-5) + C$ . Use a calculator to find the values of $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $0$ and $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $1$ . After calculating, we find that $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $2$ and $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $3$ . Now substitute these values into the equation: $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $4$ .
Find $f(6)$ : Simplifying, we have $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ . The last integral is straightforward: $\int -2\cos(x-3)dx = -2\sin(x-3)$ .Putting it all together, we have $f(x) = x^2\sin(x-3) + 2x\cos(x-3) + 2\sin(x-3) + C$ , where $C$ is the constant of integration.Now we use the initial condition $f(-2) = -4$ to solve for $C$ . Plug in $x = -2$ into the equation: $-4 = (-2)^2\sin(-2-3) + 2(-2)\cos(-2-3) + 2\sin(-2-3) + C$ .Calculate the trigonometric values and simplify: $-4 = 4\sin(-5) - 4\cos(-5) + 2\sin(-5) + C$ . Use a calculator to find the values of $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $0$ and $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $1$ .After calculating, we find that $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $2$ and $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $3$ . Now substitute these values into the equation: $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $4$ .Simplify the equation to find $C$ : $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $6$ . Now solve for $C$ : $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $8$ .
Find $f(6)$ : Simplifying, we have $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ . The last integral is straightforward: $\int -2\cos(x-3)dx = -2\sin(x-3)$ . Putting it all together, we have $f(x) = x^2\sin(x-3) + 2x\cos(x-3) + 2\sin(x-3) + C$ , where $C$ is the constant of integration. Now we use the initial condition $f(-2) = -4$ to solve for $C$ . Plug in $x = -2$ into the equation: $-4 = (-2)^2\sin(-2-3) + 2(-2)\cos(-2-3) + 2\sin(-2-3) + C$ . Calculate the trigonometric values and simplify: $-4 = 4\sin(-5) - 4\cos(-5) + 2\sin(-5) + C$ . Use a calculator to find the values of $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $0$ and $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $1$ . After calculating, we find that $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $2$ and $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $3$ . Now substitute these values into the equation: $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $4$ . Simplify the equation to find $C$ : $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $6$ . Now solve for $C$ : $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $8$ . Calculate the value of $C$ : $\int -2\cos(x-3)dx = -2\sin(x-3)$ $0$ . This is the constant of integration.
Find $f(6)$ : Simplifying, we have $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ . The last integral is straightforward: $\int -2\cos(x-3)dx = -2\sin(x-3)$ . Putting it all together, we have $f(x) = x^2\sin(x-3) + 2x\cos(x-3) + 2\sin(x-3) + C$ , where $C$ is the constant of integration. Now we use the initial condition $f(-2) = -4$ to solve for $C$ . Plug in $x = -2$ into the equation: $-4 = (-2)^2\sin(-2-3) + 2(-2)\cos(-2-3) + 2\sin(-2-3) + C$ . Calculate the trigonometric values and simplify: $-4 = 4\sin(-5) - 4\cos(-5) + 2\sin(-5) + C$ . Use a calculator to find the values of $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $0$ and $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $1$ . After calculating, we find that $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $2$ and $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $3$ . Now substitute these values into the equation: $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $4$ . Simplify the equation to find $C$ : $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $6$ . Now solve for $C$ : $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $8$ . Calculate the value of $C$ : $\int -2\cos(x-3)dx = -2\sin(x-3)$ $0$ . This is the constant of integration. Now that we have $C$ , we can find $f(6)$ by plugging $\int -2\cos(x-3)dx = -2\sin(x-3)$ $3$ into the integrated function: $\int -2\cos(x-3)dx = -2\sin(x-3)$ $4$ .
Find $f(6)$ : Simplifying, we have $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ . The last integral is straightforward: $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ . Putting it all together, we have $f(x) = x^2\sin(x-3) + 2x\cos(x-3) + 2\sin(x-3) + C$ , where $C$ is the constant of integration. Now we use the initial condition $f(-2) = -4$ to solve for $C$ . Plug in $x = -2$ into the equation: $-4 = (-2)^2\sin(-2-3) + 2(-2)\cos(-2-3) + 2\sin(-2-3) + C$ . Calculate the trigonometric values and simplify: $-4 = 4\sin(-5) - 4\cos(-5) + 2\sin(-5) + C$ . Use a calculator to find the values of $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $0$ and $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $1$ . After calculating, we find that $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $2$ and $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $3$ . Now substitute these values into the equation: $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $4$ . Simplify the equation to find $C$ : $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $6$ . Now solve for $C$ : $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $8$ . Calculate the value of $C$ : $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ $0$ . This is the constant of integration. Now that we have $C$ , we can find $f(6)$ by plugging $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ $3$ into the integrated function: $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ $4$ . Calculate the trigonometric values for $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ $5$ and $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ $6$ using a calculator, then substitute them into the equation to find $f(6)$ .
Find $f(6)$ : Simplifying, we have $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ . The last integral is straightforward: $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ . Putting it all together, we have $f(x) = x^2\sin(x-3) + 2x\cos(x-3) + 2\sin(x-3) + C$ , where $C$ is the constant of integration. Now we use the initial condition $f(-2) = -4$ to solve for $C$ . Plug in $x = -2$ into the equation: $-4 = (-2)^2\sin(-2-3) + 2(-2)\cos(-2-3) + 2\sin(-2-3) + C$ . Calculate the trigonometric values and simplify: $-4 = 4\sin(-5) - 4\cos(-5) + 2\sin(-5) + C$ . Use a calculator to find the values of $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $0$ and $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $1$ . After calculating, we find that $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $2$ and $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $3$ . Now substitute these values into the equation: $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $4$ . Simplify the equation to find $C$ : $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $6$ . Now solve for $C$ : $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $8$ . Calculate the value of $C$ : $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ $0$ . This is the constant of integration. Now that we have $C$ , we can find $f(6)$ by plugging $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ $3$ into the integrated function: $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ $4$ . Calculate the trigonometric values for $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ $5$ and $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ $6$ using a calculator, then substitute them into the equation to find $f(6)$ . After calculating, we find that $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ $8$ and $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ $9$ . Now substitute these values into the equation: $f(x) = x^2\sin(x-3) + 2x\cos(x-3) + 2\sin(x-3) + C$ $0$ .
Find $f(6)$ : Simplifying, we have $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ . The last integral is straightforward: $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ . Putting it all together, we have $f(x) = x^2\sin(x-3) + 2x\cos(x-3) + 2\sin(x-3) + C$ , where $C$ is the constant of integration. Now we use the initial condition $f(-2) = -4$ to solve for $C$ . Plug in $x = -2$ into the equation: $-4 = (-2)^2\sin(-2-3) + 2(-2)\cos(-2-3) + 2\sin(-2-3) + C$ . Calculate the trigonometric values and simplify: $-4 = 4\sin(-5) - 4\cos(-5) + 2\sin(-5) + C$ . Use a calculator to find the values of $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $0$ and $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $1$ . After calculating, we find that $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $2$ and $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $3$ . Now substitute these values into the equation: $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $4$ . Simplify the equation to find $C$ : $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $6$ . Now solve for $C$ : $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $8$ . Calculate the value of $C$ : $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ $0$ . This is the constant of integration. Now that we have $C$ , we can find $f(6)$ by plugging $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ $3$ into the integrated function: $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ $4$ . Calculate the trigonometric values for $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ $5$ and $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ $6$ using a calculator, then substitute them into the equation to find $f(6)$ . After calculating, we find that $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ $8$ and $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ $9$ . Now substitute these values into the equation: $f(x) = x^2\sin(x-3) + 2x\cos(x-3) + 2\sin(x-3) + C$ $0$ . Simplify the equation to find $f(6)$ : $f(x) = x^2\sin(x-3) + 2x\cos(x-3) + 2\sin(x-3) + C$ $2$ . Now calculate the sum to get the value of $f(6)$ .
Find $f(6)$ : Simplifying, we have $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ . The last integral is straightforward: $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ . Putting it all together, we have $f(x) = x^2\sin(x-3) + 2x\cos(x-3) + 2\sin(x-3) + C$ , where $C$ is the constant of integration. Now we use the initial condition $f(-2) = -4$ to solve for $C$ . Plug in $x = -2$ into the equation: $-4 = (-2)^2\sin(-2-3) + 2(-2)\cos(-2-3) + 2\sin(-2-3) + C$ . Calculate the trigonometric values and simplify: $-4 = 4\sin(-5) - 4\cos(-5) + 2\sin(-5) + C$ . Use a calculator to find the values of $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $0$ and $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $1$ . After calculating, we find that $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $2$ and $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $3$ . Now substitute these values into the equation: $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $4$ . Simplify the equation to find $C$ : $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $6$ . Now solve for $C$ : $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)\,dx$ $8$ . Calculate the value of $C$ : $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ $0$ . This is the constant of integration. Now that we have $C$ , we can find $f(6)$ by plugging $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ $3$ into the integrated function: $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ $4$ . Calculate the trigonometric values for $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ $5$ and $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ $6$ using a calculator, then substitute them into the equation to find $f(6)$ . After calculating, we find that $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ $8$ and $\int -2\cos(x-3)\,dx = -2\sin(x-3)$ $9$ . Now substitute these values into the equation: $f(x) = x^2\sin(x-3) + 2x\cos(x-3) + 2\sin(x-3) + C$ $0$ . Simplify the equation to find $f(6)$ : $f(x) = x^2\sin(x-3) + 2x\cos(x-3) + 2\sin(x-3) + C$ $2$ . Now calculate the sum to get the value of $f(6)$ . Calculate the value of $f(6)$ : $f(x) = x^2\sin(x-3) + 2x\cos(x-3) + 2\sin(x-3) + C$ $5$ . Round to the nearest thousandth.
Find $f(6)$ : Simplifying, we have $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ . The last integral is straightforward: $\int -2\cos(x-3)dx = -2\sin(x-3)$ .Putting it all together, we have $f(x) = x^2\sin(x-3) + 2x\cos(x-3) + 2\sin(x-3) + C$ , where $C$ is the constant of integration.Now we use the initial condition $f(-2) = -4$ to solve for $C$ . Plug in $x = -2$ into the equation: $-4 = (-2)^2\sin(-2-3) + 2(-2)\cos(-2-3) + 2\sin(-2-3) + C$ .Calculate the trigonometric values and simplify: $-4 = 4\sin(-5) - 4\cos(-5) + 2\sin(-5) + C$ . Use a calculator to find the values of $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $0$ and $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $1$ .After calculating, we find that $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $2$ and $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $3$ . Now substitute these values into the equation: $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $4$ .Simplify the equation to find $C$ : $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $6$ . Now solve for $C$ : $f(x) = x^2\sin(x-3) + 2x\cos(x-3) - \int -2\cos(x-3)dx$ $8$ .Calculate the value of $C$ : $\int -2\cos(x-3)dx = -2\sin(x-3)$ $0$ . This is the constant of integration.Now that we have $C$ , we can find $f(6)$ by plugging $\int -2\cos(x-3)dx = -2\sin(x-3)$ $3$ into the integrated function: $\int -2\cos(x-3)dx = -2\sin(x-3)$ $4$ .Calculate the trigonometric values for $\int -2\cos(x-3)dx = -2\sin(x-3)$ $5$ and $\int -2\cos(x-3)dx = -2\sin(x-3)$ $6$ using a calculator, then substitute them into the equation to find $f(6)$ .After calculating, we find that $\int -2\cos(x-3)dx = -2\sin(x-3)$ $8$ and $\int -2\cos(x-3)dx = -2\sin(x-3)$ $9$ . Now substitute these values into the equation: $f(x) = x^2\sin(x-3) + 2x\cos(x-3) + 2\sin(x-3) + C$ $0$ .Simplify the equation to find $f(6)$ : $f(x) = x^2\sin(x-3) + 2x\cos(x-3) + 2\sin(x-3) + C$ $2$ . Now calculate the sum to get the value of $f(6)$ .Calculate the value of $f(6)$ : $f(x) = x^2\sin(x-3) + 2x\cos(x-3) + 2\sin(x-3) + C$ $5$ . Round to the nearest thousandth.The value of $f(6)$ to the nearest thousandth is approximately $f(x) = x^2\sin(x-3) + 2x\cos(x-3) + 2\sin(x-3) + C$ $7$ .

The derivative of the function f f f is defined by f′(x)=x2cos⁡(x−3) f^{\prime}(x)=x^{2} \cos (x-3) f′(x)=x2cos(x−3). If f(−2)=−4 f(-2)=-4 f(−2)=−4, then use a calculator to find the value of f(6) f(6) f(6) to the nearest thousandth.\newlineAnswer:

The derivative of the function $f$ is defined by $f^{\prime}(x)=x^{2} \cos (x-3)$ . If $f(-2)=-4$ , then use a calculator to find the value of $f(6)$ to the nearest thousandth. $\newline$ Answer: