AI tutor
Full solution
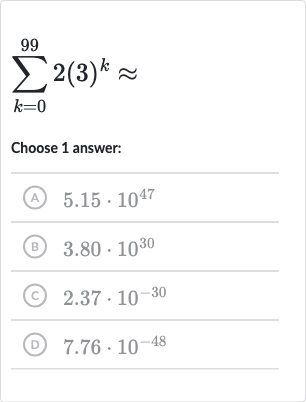
Q. Choose answer:(A) (B) (C) (D)
- Identify series type: Identify the type of series.The series is a geometric series because each term is obtained by multiplying the previous term by a common ratio, which in this case is .
- Use formula for sum: Use the formula for the sum of a finite geometric series.The sum of a geometric series can be calculated using the formula , where is the first term, is the common ratio, and is the number of terms.
- Calculate first term: Calculate the first term of the series.The first term when is .
- Calculate number of terms: Calculate the number of terms in the series.Since the series starts at and goes to , there are terms in total.
- Calculate sum using formula: Calculate the sum using the formula.
- Simplify expression: Simplify the expression.
- Further simplify expression: Further simplify the expression.
- Evaluate expression: Evaluate the expression.Since is a very large number, we can approximate it using scientific notation. However, we do not have the exact value of , so we cannot directly calculate the answer. We need to estimate or use a calculator to find the value in scientific notation.
- Use calculator for scientific notation: Use a calculator or estimation to find in scientific notation.Assuming we use a calculator, we find that is approximately .
- Subtract from calculated value: Subtract from the calculated value to find the sum.Since subtracting from such a large number does not significantly change the value, we can say that is approximately .
More problems from Compare linear and exponential growth
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help