AI tutor
Full solution
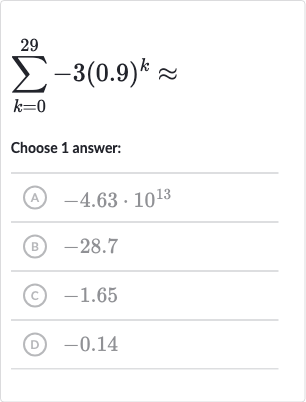
Q. Choose answer:(A) (B) .(C) .(D) .
- Identify series type: Identify the type of series. The series given is a geometric series because each term is obtained by multiplying the previous term by a common ratio, which is in this case.
- Use formula for sum: Use the formula for the sum of a finite geometric series.The sum of a geometric series with first term , common ratio (where |r| < 1), and terms is given by the formula:Here, (the first term), (the common ratio), and (since we are summing from to ).
- Plug values and calculate: Plug the values into the formula and calculate the sum.Now we need to calculate and then the rest of the expression.
- Calculate : Calculate . is a very small number, and for practical purposes, we can consider it to be close to when subtracted from , given the context of the other answer choices. However, for accuracy, we should still calculate it.
- Calculate sum using approximation: Calculate the sum using the approximation that is close to .
- Check answer choices: Check the answer choices for the closest value to our calculation.The closest value to is (B) . Therefore, the sum of the series is approximately .
More problems from Compare linear and exponential growth
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help