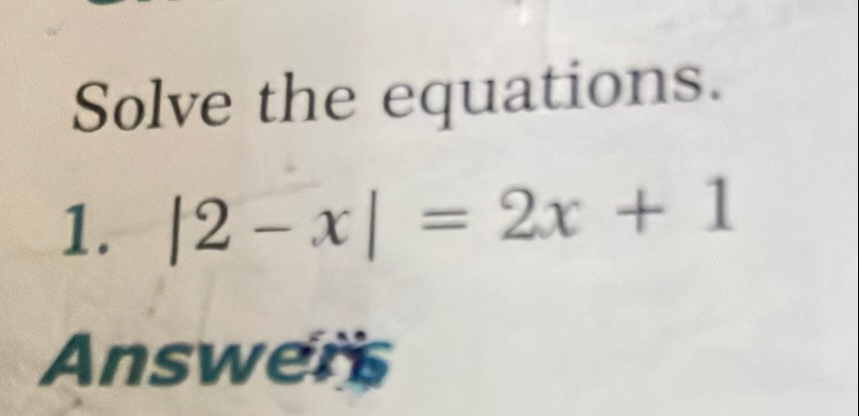Solve the equations. |2-x|=2x+1

Question

Bytelearn · Accepted Answer

Understand absolute value equation: Understand the absolute value equation. The absolute value of a number is its distance from zero on the number line, regardless of direction. Therefore, |2-x| can be either 2-x or x-2, depending on the value of x. We need to consider both cases to solve the equation |2-x|=2x+1.Set up two equations: Set up two separate equations to solve, one for each case of the absolute value. Case 1: 2 - x = 2x + 1 Case 2: x - 2 = 2x + 1Solve first case: Solve the first case. 2 - x = 2x + 1 Move all terms involving x to one side and constant terms to the other side. 2 - 1 = 2x + x 1 = 3x Now, divide both sides by 3 to solve for x. x = 1/3Solve second case: Solve the second case. x - 2 = 2x + 1 Move all terms involving x to one side and constant terms to the other side. -2 - 1 = 2x - x -3 = x x = -3Check solutions: Check both solutions in the original equation to ensure they do not result in a negative inside the absolute value equaling a positive number, as this would be a math error. For x = 1/3: |2 - (1/3)| = 2*(1/3) + 1 |5/3| = 2/3 + 1 5/3 = 2/3 + 3/3 5/3 = 5/3 This is true, so x = 1/3 is a valid solution.  For x = -3: |2 - (-3)| = 2*(-3) + 1 |2 + 3| = -6 + 1 |5| = -5 5 ≠ -5 This is not true, so x = -3 is not a valid solution.

Solve the equations. $\newline$ $|2-x|=2 x+1$

Full solution

More problems from Add and subtract rational numbers

Related topics

Solve the equations.\newline∣2−x∣=2x+1 |2-x|=2 x+1 ∣2−x∣=2x+1

Solve the equations. $\newline$ $|2-x|=2 x+1$