AI tutor
Full solution
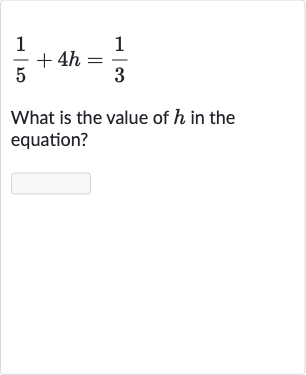
Q. What is the value of in the equation?
- Isolate variable h: First, we need to isolate the variable h on one side of the equation. To do this, we will subtract from both sides of the equation to get by itself.
- Calculate right side: Now, we calculate the right side of the equation by finding a common denominator for and , which is . Then we subtract the fractions.
- Equation simplification: The equation now looks like this:
- Divide by : To find the value of , we divide both sides of the equation by .
- Multiply by reciprocal: Dividing by is the same as multiplying by the reciprocal of , which is . So we multiply by .
- Multiply numerators and denominators: Now we multiply the numerators and the denominators separately.
- Simplify fraction: Finally, we simplify the fraction by dividing both the numerator and the denominator by their greatest common divisor, which is .