AI tutor
Full solution
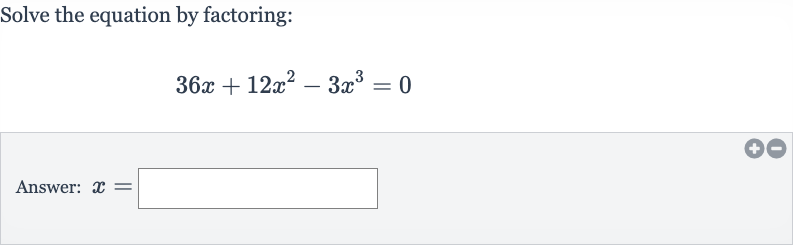
Q. Solve the equation by factoring:Answer:
- Rearrange Equation: First, we need to rearrange the equation in standard polynomial form, which is usually written from the highest power to the lowest power of . So, we rewrite the equation as:
- Factor Out GCF: Next, we can factor out the greatest common factor (GCF) from each term. The GCF in this case is , so we factor it out:
- Factor Quadratic Expression: Now, we need to factor the quadratic expression inside the parentheses. We are looking for two numbers that multiply to (the constant term) and add up to (the coefficient of the term). Those numbers are and . So, we can write the factored form as:
- Set Equations and Solve: To find the solutions, we set each factor equal to zero and solve for : or or
- Find Solutions: Solving each equation for gives us the solutions: or or Simplifying gives us .So, the solutions are , , and .
More problems from Operations with rational exponents
QuestionGet tutor help
QuestionGet tutor help