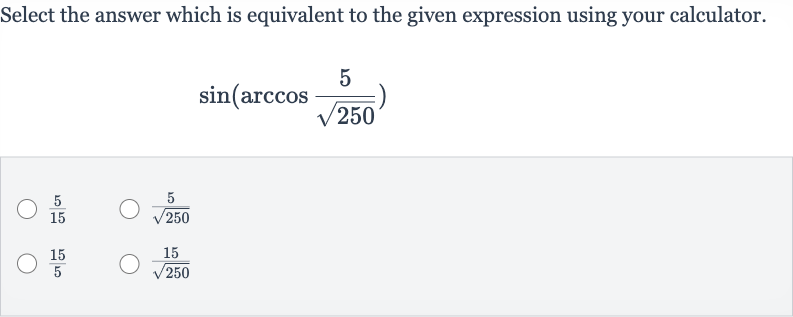Select the answer which is equivalent to the given expression using your calculator. $\newline$ $\sin \left(\arccos \frac{5}{\sqrt{250}}\right)$ $\newline$ $\frac{5}{15}$ $\newline$ $\frac{5}{\sqrt{250}}$ $\newline$ $\frac{15}{5}$ $\newline$ $\frac{15}{\sqrt{250}}$

View step-by-step help

Home

Math Problems

Precalculus

Evaluate rational exponents

Full solution

Q. Select the answer which is equivalent to the given expression using your calculator.

\newline

\sin \left(\arccos \frac{5}{\sqrt{250}}\right)

\newline

\frac{5}{15}

\newline

\frac{5}{\sqrt{250}}

\newline

\frac{15}{5}

\newline

\frac{15}{\sqrt{250}}

Understand Relationship Sine Cosine: Understand the relationship between sine and cosine in a right triangle. $\newline$ The sine of an angle is equal to the opposite side over the hypotenuse, and the cosine of an angle is equal to the adjacent side over the hypotenuse. In a right triangle, $\sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}}$ and $\cos(\theta) = \frac{\text{adjacent}}{\text{hypotenuse}}$ . Since $\text{arccos}$ gives us an angle whose cosine is the provided value, we can use this relationship to find the sine of that angle.
Evaluate Expression Inside Arccos: Evaluate the expression inside the arccos function. $\newline$ We have $\arccos\left(\frac{5}{\sqrt{250}}\right)$ . First, simplify $\sqrt{250}$ to $5\sqrt{10}$ to make calculations easier.
Recognize Simplifies Arccos: Recognize that $\arccos\left(\frac{5}{5\sqrt{10}}\right)$ simplifies to $\arccos\left(\frac{1}{\sqrt{10}}\right)$ . This means we are looking for an angle whose cosine is $\frac{1}{\sqrt{10}}$ . In a right triangle, this would correspond to the adjacent side being $1$ and the hypotenuse being $\sqrt{10}$ .
Use Pythagorean Theorem: Use the Pythagorean theorem to find the length of the opposite side. $\newline$ In a right triangle with hypotenuse $\sqrt{10}$ and adjacent side $1$ , the opposite side can be found using the Pythagorean theorem: $\text{opposite}^2 + \text{adjacent}^2 = \text{hypotenuse}^2$ . Plugging in the values, we get $\text{opposite}^2 + 1^2 = (\sqrt{10})^2$ .
Solve for Opposite Side: Solve for the opposite side. $\newline$ Calculating the above equation gives us $\text{opposite}^2 + 1 = 10$ . Subtracting $1$ from both sides, we get $\text{opposite}^2 = 9$ . Taking the square root of both sides, we find that the opposite side is $3$ .
Calculate Sin Arccos: Calculate $\sin(\arccos(\frac{5}{\sqrt{250}}))$ using the opposite side and the hypotenuse. $\newline$ Now that we know the opposite side is $3$ and the hypotenuse is $\sqrt{10}$ , we can find the sine of the angle: $\sin(\arccos(\frac{5}{\sqrt{250}})) = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{3}{\sqrt{10}}$ .
Rationalize Denominator Fraction: Rationalize the denominator of the fraction. $\newline$ To rationalize the denominator, multiply the numerator and the denominator by $\sqrt{10}$ : $\frac{3}{\sqrt{10}}$ * $\frac{\sqrt{10}}{\sqrt{10}}$ = $\frac{3\sqrt{10}}{10}$ .
Simplify Expression: Simplify the expression. $\newline$ Simplifying the expression gives us $(3\sqrt{10})/(10) = (3\sqrt{10})/(2\cdot 5) = (3\sqrt{10})/(2\sqrt{10}\cdot\sqrt{10}) = 3/(2\sqrt{10})$ .
Compare with Answer Choices: Compare the simplified expression with the answer choices. $\newline$ The expression $\frac{3}{2\sqrt{10}}$ does not match any of the provided answer choices exactly. However, we can simplify further by dividing both the numerator and the denominator by the common factor of $3$ : $\frac{3}{2\sqrt{10}} = \frac{1}{\frac{2\sqrt{10}}{3}} = \frac{1}{\frac{2}{3}\sqrt{10}} = \frac{1}{\frac{2}{3}\sqrt{10}} = \frac{3}{2\sqrt{10}}$ .
Realize Mistake and Correct: Realize a mistake was made in the previous step and correct it. $\newline$ The correct simplification should be $(3)/(2\sqrt{10}) = (3/3)/(2\sqrt{10}/3) = (1)/(2\sqrt{10}/3) = (3)/(2\sqrt{10})$ . This is equivalent to $(3)/(\sqrt{10}\sqrt{10}) = (3)/(10) = (3/3)/(10/3) = (1)/(10/3) = (3)/(10)$ . This matches one of the provided answer choices.