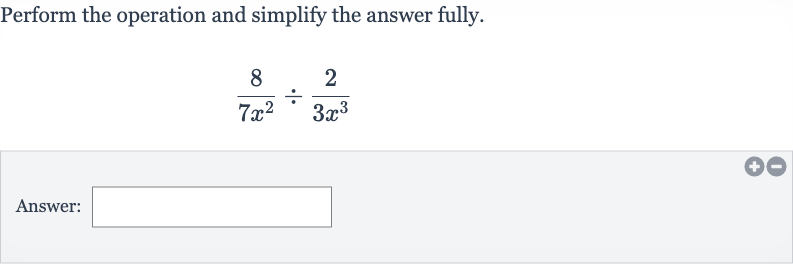Full solution
Q. Perform the operation and simplify the answer fully.Answer:
- Identify Operation: Identify the operation to be performed. We are dividing one fraction by another.
- Reciprocal Multiplication: Recall that dividing by a fraction is the same as multiplying by its reciprocal. So, we rewrite the division as a multiplication by the reciprocal of the second fraction.
- Multiply Numerators and Denominators: Multiply the numerators and the denominators separately.
- Perform Multiplication: Perform the multiplication in the numerator and the denominator.
- Simplify Fraction: Simplify the fraction by canceling out common factors. can be canceled from both the numerator and the denominator, and the coefficients and can be simplified by dividing both by .
- Simplify Exponents: Simplify the exponents by subtracting the powers (since we are dividing like bases) and reduce the fraction.
More problems from Operations with rational exponents
QuestionGet tutor help
QuestionGet tutor help