Full solution
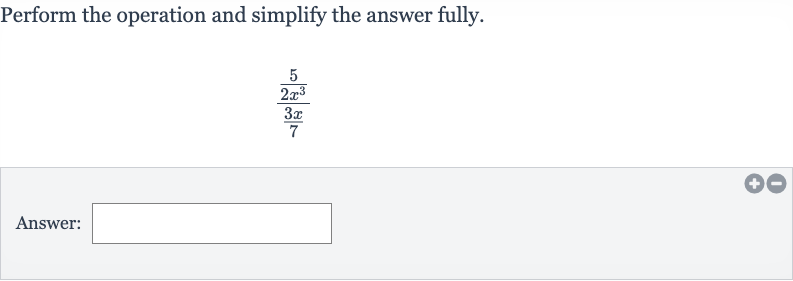
Q. Perform the operation and simplify the answer fully.Answer:
- Identify Given Expression: Identify the given expression and rewrite it as a single fraction by multiplying by the reciprocal of the denominator.The expression is /. To divide by a fraction, we multiply by its reciprocal.So, is the expression we will simplify.
- Multiply Numerators and Denominators: Multiply the numerators and the denominators separately. for the numerators and for the denominators.So, the expression becomes .
- Check for Further Simplification: Check if the fraction can be simplified further. The numbers and have no common factors other than , and the variable part cannot be simplified further. Therefore, the expression is already in its simplest form.
More problems from Operations with rational exponents
QuestionGet tutor help
QuestionGet tutor help