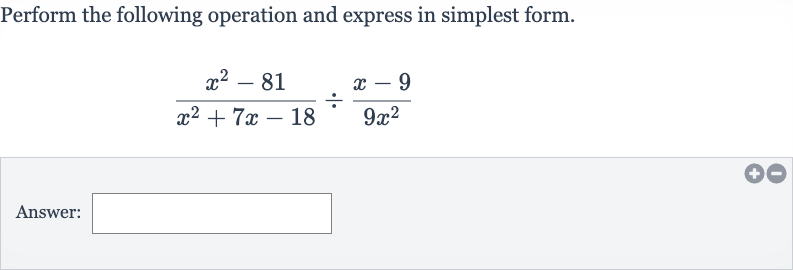Perform the following operation and express in simplest form. (x^(2)-81)/(x^(2)+7x-18)÷(x-9)/(9x^(2)) Answer:

Question

Perform the following operation and express in simplest form.  (x^(2)-81)/(x^(2)+7x-18)÷(x-9)/(9x^(2)) Answer:

Bytelearn · Accepted Answer

Identify Operation and Rewrite: Identify the operation to be performed and rewrite the division as multiplication by the reciprocal. The given expression is a division of two fractions, which can be rewritten as the multiplication of the first fraction by the reciprocal of the second fraction. (x^(2)-81)/(x^(2)+7x-18) * (9x^(2))/(x-9)Factor Numerator and Denominator: Factor the numerator and denominator of the first fraction where possible. The numerator x^2 - 81 is a difference of squares and can be factored as (x + 9)(x - 9). The denominator x^2 + 7x - 18 can be factored by finding two numbers that multiply to -18 and add to 7, which are 9 and -2. So, x^2 + 7x - 18 factors as (x + 9)(x - 2). Now the expression is ((x + 9)(x - 9))/((x + 9)(x - 2)) * (9x^(2))/(x-9).Cancel Common Factors: Cancel out common factors in the first fraction. The (x + 9) terms cancel out in the numerator and denominator of the first fraction. Now the expression is (x - 9)/(x - 2) * (9x^(2))/(x-9).Multiply Remaining Terms: Cancel out the common (x - 9) terms in the resulting expression. The (x - 9) terms cancel out in the numerator of the first fraction and the denominator of the second fraction. Now the expression is 1/(x - 2) * (9x^(2))/1.Check for Simplification: Multiply the remaining terms. Multiplying the remaining terms gives us 9x^2/(x - 2).Check for any further simplification. The expression 9x^2/(x - 2) cannot be simplified further as there are no common factors to cancel out.

Perform the following operation and express in simplest form. $\newline$ $\frac{x^{2}-81}{x^{2}+7 x-18} \div \frac{x-9}{9 x^{2}}$ $\newline$ Answer:

Full solution

More problems from Operations with rational exponents

Related topics

Perform the following operation and express in simplest form.\newlinex2−81x2+7x−18÷x−99x2 \frac{x^{2}-81}{x^{2}+7 x-18} \div \frac{x-9}{9 x^{2}} x2+7x−18x2−81​÷9x2x−9​\newlineAnswer:

Perform the following operation and express in simplest form. $\newline$ $\frac{x^{2}-81}{x^{2}+7 x-18} \div \frac{x-9}{9 x^{2}}$ $\newline$ Answer: