AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
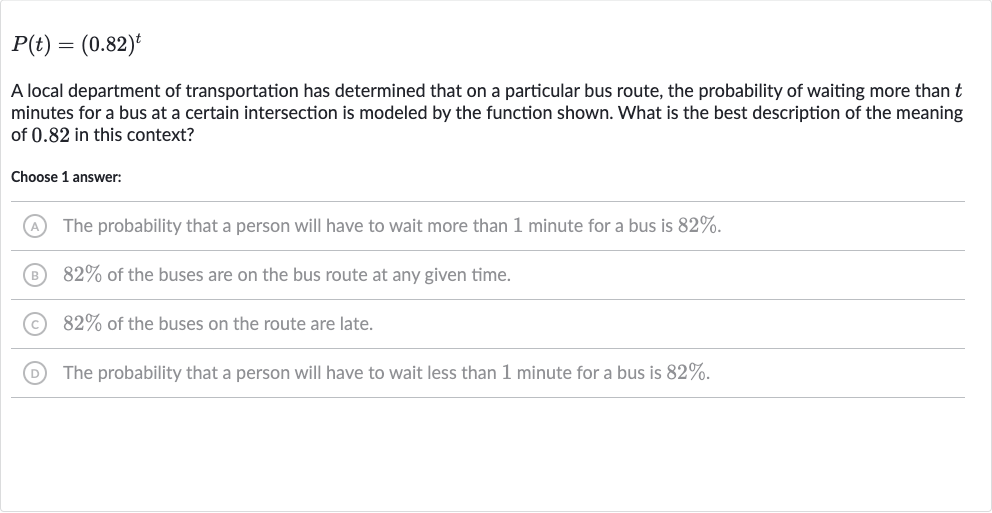
A local department of transportation has determined that on a particular bus route, the probability of waiting more than minutes for a bus at a certain intersection is modeled by the function shown. What is the best description of the meaning of . in this context?Choose answer:(A) The probability that a person will have to wait more than minute for a bus is .(B) of the buses are on the bus route at any given time.(C) of the buses on the route are late.(D) The probability that a person will have to wait less than minute for a bus is .
Full solution
Q. A local department of transportation has determined that on a particular bus route, the probability of waiting more than minutes for a bus at a certain intersection is modeled by the function shown. What is the best description of the meaning of . in this context?Choose answer:(A) The probability that a person will have to wait more than minute for a bus is .(B) of the buses are on the bus route at any given time.(C) of the buses on the route are late.(D) The probability that a person will have to wait less than minute for a bus is .
- Calculate Probability for : The function gives the probability of waiting more than minutes for a bus. To understand what means, we look at the case when .
- Interpret Probability Value: Calculate to see the probability of waiting more than minute. , which means there's an chance of waiting more than minute.
- Describe Probability: Since is , the best description of is the probability that a person will have to wait more than minute for a bus.
More problems from Evaluate two-variable equations: word problems
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
