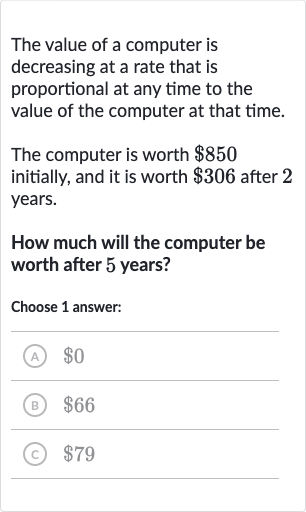
The value of a computer is decreasing at a rate that is proportional at any time to the value of the computer at that time. $\newline$ The computer is worth $\$ 850$ initially, and it is worth $\$ 306$ after $2$ years. $\newline$ How much will the computer be worth after $5$ years? $\newline$ Choose $1$ answer: $\newline$ (A) $\$ 0$ $\newline$ (B) $\$ 66$ $\newline$ (C) $\$ 79$

View step-by-step help

Home

Math Problems

Grade 7

Evaluate two-variable equations: word problems

Full solution

Q. The value of a computer is decreasing at a rate that is proportional at any time to the value of the computer at that time.

\newline

The computer is worth

\$ 850

initially, and it is worth

\$ 306

after

2

years.

\newline

How much will the computer be worth after

5

years?

\newline

Choose

1

answer:

\newline

(A)

\$ 0

\newline

(B)

\$ 66

\newline

(C)

\$ 79

Exponential Decay Model: We are given that the value of the computer decreases proportionally to its current value, which suggests that the depreciation follows an exponential decay model. The general formula for exponential decay is: $\newline$ $V(t) = V_0 \cdot e^{(-kt)}$ $\newline$ where: $\newline$ - $V(t)$ is the value of the computer at time $t$ , $\newline$ - $V_0$ is the initial value of the computer, $\newline$ - $k$ is the decay constant, $\newline$ - $t$ is the time in years, $\newline$ - $e$ is the base of the natural logarithm. $\newline$ We need to find the decay constant $k$ using the initial value and the value after $2$ years.
Initial Values: First, let's plug in the values we know into the exponential decay formula to find $k$ . We know that V_0 = $850 and V(2) = $306 . So, we have: $\newline$ $306 = 850 \cdot e^{(-2k)}$ $\newline$ Now, we need to solve for $k$ .
Solving for k: To solve for $k$ , we first divide both sides of the equation by $850$ : $\newline$ $\frac{306}{850} = e^{(-2k)}$
Calculating k: Next, we take the natural logarithm of both sides to get rid of the exponential: $\newline$ $\ln\left(\frac{306}{850}\right) = \ln\left(e^{(-2k)}\right)$ $\newline$ $\ln\left(\frac{306}{850}\right) = -2k \cdot \ln(e)$ $\newline$ Since $\ln(e) = 1$ , we can simplify this to: $\newline$ $\ln\left(\frac{306}{850}\right) = -2k$
Finding Value after $5$ Years: Now we solve for $k$ by dividing both sides by $-2$ : $\newline$ $k = \frac{-\ln\left(\frac{306}{850}\right)}{2}$ $\newline$ Let's calculate the value of $k$ .
Finding Value after $5$ Years: Now we solve for $k$ by dividing both sides by $-2$ : $\newline$ $k = \frac{-\ln\left(\frac{306}{850}\right)}{2}$ $\newline$ Let's calculate the value of $k$ .Using a calculator, we find: $\newline$ $k = \frac{-\ln\left(\frac{306}{850}\right)}{2} \approx \frac{-\ln(0.36)}{2} \approx \frac{-(-1.02165)}{2} \approx 0.510825$
Finding Value after $5$ Years: Now we solve for $k$ by dividing both sides by $-2$ : $\newline$ $k = \frac{-\ln\left(\frac{306}{850}\right)}{2}$ $\newline$ Let's calculate the value of $k$ .Using a calculator, we find: $\newline$ $k = \frac{-\ln\left(\frac{306}{850}\right)}{2} \approx \frac{-\ln(0.36)}{2} \approx \frac{-(-1.02165)}{2} \approx 0.510825$ Now that we have the decay constant $k$ , we can use it to find the value of the computer after $5$ years. We plug $k$ , $V_0$ , and $t = 5$ into the exponential decay formula: $\newline$ $V(5) = 850 \cdot e^{(-0.510825 \cdot 5)}$ $\newline$ Let's calculate $V(5)$ .
Finding Value after $5$ Years: Now we solve for $k$ by dividing both sides by $-2$ : $\newline$ $k = \frac{-\ln\left(\frac{306}{850}\right)}{2}$ $\newline$ Let's calculate the value of $k$ .Using a calculator, we find: $\newline$ $k = \frac{-\ln\left(\frac{306}{850}\right)}{2} \approx \frac{-\ln(0.36)}{2} \approx \frac{-(-1.02165)}{2} \approx 0.510825$ Now that we have the decay constant $k$ , we can use it to find the value of the computer after $5$ years. We plug $k$ , $V_0$ , and $t = 5$ into the exponential decay formula: $\newline$ $V(5) = 850 \cdot e^{(-0.510825 \cdot 5)}$ $\newline$ Let's calculate $V(5)$ .Using a calculator, we find: $\newline$ $V(5) = 850 \cdot e^{(-0.510825 \cdot 5)} \approx 850 \cdot e^{(-2.554125)} \approx 850 \cdot 0.0776 \approx 65.96$
Finding Value after $5$ Years: Now we solve for $k$ by dividing both sides by $-2$ : $\newline$ $k = \frac{-\ln\left(\frac{306}{850}\right)}{2}$ $\newline$ Let's calculate the value of $k$ .Using a calculator, we find: $\newline$ $k = \frac{-\ln\left(\frac{306}{850}\right)}{2} \approx \frac{-\ln(0.36)}{2} \approx \frac{-(-1.02165)}{2} \approx 0.510825$ Now that we have the decay constant $k$ , we can use it to find the value of the computer after $5$ years. We plug $k$ , $V_0$ , and $t = 5$ into the exponential decay formula: $\newline$ $V(5) = 850 \cdot e^{(-0.510825 \cdot 5)}$ $\newline$ Let's calculate $V(5)$ .Using a calculator, we find: $\newline$ $V(5) = 850 \cdot e^{(-0.510825 \cdot 5)} \approx 850 \cdot e^{(-2.554125)} \approx 850 \cdot 0.0776 \approx 65.96$ The value $65.96$ is close to $66 , which is one of the given answer choices. Since the value of the computer cannot be exactly $66 due to rounding during calculations, we choose the closest answer, which is $66 .