Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

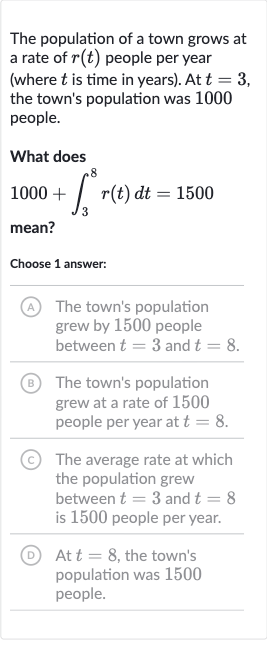
The population of a town grows at a rate of r(t) people per year (where t is time in years). At t=3, the town's population was 1000 people. What does 1000+int_(3)^(8)r(t)dt=1500 mean? Choose 1 answer: (A) The town's population grew by 1500 people between t=3 and t=8. B The town's population grew at a rate of 1500 people per year at t=8. (C) The average rate at which the population grew between t=3 and t=8 is 1500 people per year. (D) At t=8, the town's population was 1500 people.

The population of a town grows at a rate of r(t) r(t) people per year (where t t is time in years). At t=3 t=3 , the town's population was 10001000 people.\newlineWhat does 1000+∫38r(t)dt=1500 1000+\int_{3}^{8} r(t) d t=1500 mean?\newlineChoose 11 answer:\newline(A) The town's population grew by 15001500 people between t=3 t=3 and t=8 t=8 .\newline(B) The town's population grew at a rate of 15001500 people per year at t=8 t=8 .\newline(C) The average rate at which the population grew between t=3 t=3 and t=8 t=8 is 15001500 people per year.\newline(D) At t=8 t=8 , the town's population was 15001500 people.

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Grade 7right chevron icon
Evaluate two-variable equations: word problemsright chevron icon

Full solution

Q. The population of a town grows at a rate of r(t) r(t) people per year (where t t is time in years). At t=3 t=3 , the town's population was 10001000 people.\newlineWhat does 1000+∫38r(t)dt=1500 1000+\int_{3}^{8} r(t) d t=1500 mean?\newlineChoose 11 answer:\newline(A) The town's population grew by 15001500 people between t=3 t=3 and t=8 t=8 .\newline(B) The town's population grew at a rate of 15001500 people per year at t=8 t=8 .\newline(C) The average rate at which the population grew between t=3 t=3 and t=8 t=8 is 15001500 people per year.\newline(D) At t=8 t=8 , the town's population was 15001500 people.
  1. Understand integral expression: Understand the integral expression.\newlineThe integral ∫38r(t) dt\int_{3}^{8} r(t) \, dt represents the total population growth from time t=3t=3 to t=8t=8. The function r(t)r(t) is the rate of population growth per year, and the integral sums up this growth rate over the time interval from 33 to 88 years.
  2. Interpret the equation: Interpret the equation.\newlineThe equation 1000+∫38r(t)dt=15001000 + \int_{3}^{8}r(t)dt = 1500 means that if we start with a population of 10001000 people at time t=3t=3 and add the total population growth from t=3t=3 to t=8t=8, we end up with a population of 15001500 people at time t=8t=8.
  3. Analyze answer choices: Analyze the answer choices.\newline(A) This choice suggests that the population grew by 15001500 people between t=3t=3 and t=8t=8. This is incorrect because the equation states that the population was 10001000 at t=3t=3 and became 15001500 at t=8t=8, which means the growth was 500500 people, not 15001500.
  4. Continue analyzing choices: Continue analyzing the answer choices.\newline(B) This choice suggests that the population grew at a rate of 15001500 people per year at t=8t=8. This is incorrect because the equation does not provide information about the rate of growth at a specific time, only the total growth over a period.
  5. Continue analyzing choices: Continue analyzing the answer choices.\newline(C) This choice suggests that the average rate of population growth between t=3t=3 and t=8t=8 is 15001500 people per year. This is incorrect because the total growth over the 55-year period is 500500 people, not 15001500.
  6. Continue analyzing choices: Continue analyzing the answer choices.\newline(D) This choice suggests that at t=8t=8, the town's population was 15001500 people. This is correct because the equation shows that starting with a population of 10001000 at t=3t=3 and adding the growth from t=3t=3 to t=8t=8 results in a population of 15001500 at t=8t=8.

More problems from Evaluate two-variable equations: word problems

Question
The function b(t) b(t) gives the temperature (in degrees Celsius) of a pan of brownies by time t t (in minutes).\newlineWhat does ∫06b′(t)dt=93 \int_{0}^{6} b^{\prime}(t) d t=93 mean?\newlineChoose 11 answer:\newline(A) At t=6 t=6 minutes, the temperature of the brownies is 9393 degrees Celsius.\newlineB) At t=6 t=6 minutes, the brownies have an instantaneous rate of temperature change of 9393 degrees Celsius per minute.\newline(C) During the first six minutes, the temperature of the brownies increases an average of 9393 degrees Celsius per minute.\newline(D) The temperature of the brownies increased by 9393 degrees Celsius in the first six minutes.
Get tutor helpright-arrow

Posted 7 months ago

Question
The number of subscribers to a magazine is changing at a rate of r(t) r(t) subscribers per month (where t t is time in months).\newlineWhat does ∫810r′(t)dt=7 \int_{8}^{10} r^{\prime}(t) d t=7 mean?\newlineChoose 11 answer:\newline(A) As of month 1010 , the magazine had 77 subscribers.\newline(B) The average rate of change in subscribers between month 88 and month 1010 was 77 subscribers per month.\newline(C) The number of subscribers increased by 77 between t=8 t=8 and t=10 t=10 months.\newline(D) The rate of change of number of subscribers increased by 77 subscribers per month between t=8 t=8 and t=10 t=10 months.
Get tutor helpright-arrow

Posted 7 months ago

Question
A grocery store receives a shipment of bananas. The percent of the shipment that is still suitable for sale is decreasing at a rate of r(t) r(t) percent of the original shipment per day (where t t is the time in days). At t=2 t=2 , the grocery store found 85% 85 \% of the shipment to be suitable for sale.\newlineWhat does 0.85+∫24r(t)dt=0.6 mean?  0.85+\int_{2}^{4} r(t) d t=0.6 \text { mean? } \newlineChoose 11 answer:\newline(A) As of the fourth day, 60% 60 \% of the bananas suitable on the second day are still suitable.\newline(B) Between the second and fourth days, 60% 60 \% of the remaining bananas became unsuitable for sale per day.\newline(C) Between the second and fourth day, another 60% 60 \% of the bananas became unsuitable for sale.\newline(D) As of the fourth day, 60% 60 \% of the shipment was still suitable for sale.
Get tutor helpright-arrow

Posted 7 months ago

Question
The number of people exposed to a certain illness is increasing at a rate of r(t) r(t) people per day (where t t is the time in days). At t=12 t=12 , there were 115115 people exposed to the illness.\newlineWhat does 115+∫1220r(t)dt 115+\int_{12}^{20} r(t) d t represent?\newlineChoose 11 answer:\newline(A) The change in the number of people exposed to the illness between days 1212 and 2020\newline(B) The change in the rate at which people are exposed to the illness between days 1212 and 2020\newline(C) The time it takes for 2020 more people to be exposed to the illness\newline(D) The number of people exposed to the illness at t=20 t=20
Get tutor helpright-arrow

Posted 7 months ago

Question
The value of a computer is decreasing at a rate that is proportional at any time to the value of the computer at that time.\newlineThe computer is worth $850 \$ 850 initially, and it is worth $306 \$ 306 after 22 years.\newlineHow much will the computer be worth after 55 years?\newlineChoose 11 answer:\newline(A) $0 \$ 0 \newline(B) $66 \$ 66 \newline(C) $79 \$ 79
Get tutor helpright-arrow

Posted 7 months ago

Question
The expression 11(1.022)t 11(1.022)^{t} models the per capita gross domestic product (GDP) of the US, in thousands of dollars, as a function of the number of years since 19501950 .\newlineWhat does 11.022022 represent in this expression?\newlineChoose 11 answer:\newline(A) The per capita GDP in the US was $1022 \$ 1022 in 19501950.\newline(B) The maximum per capita GDP occurred 11.022022 years after 19501950 .\newline(C) The per capita GDP in the US is multiplied by approximately 11.022022 each year.
Get tutor helpright-arrow

Posted 7 months ago

Question
Carbon dating involves the measurement of the amount of carbon−14-14 in a sample. Archaeologists sometimes use carbon dating to estimate the number of years since an organism died. The function shows the ratio, R(t) R(t) , of carbon−14-14 remaining in a sample to the original amount of carbon−14-14 after t t years.\newlineR(t)=2−0.00175t R(t)=2^{-0.00175 t} \newlineIf one sample was 33 times as old as another sample of the same material, how would the carbon−14-14 ratios of the samples relate?\newlineChoose 11 answer:\newline(A) The ratio of the older sample would be 33 times the ratio of the newer sample.\newline(B) The ratio of the newer sample would be 33 times the ratio of the older sample.\newline(C) The ratio of the older sample would be the cube of the ratio of the newer sample.\newline(D) The ratio of the newer sample would be the cube of the ratio of the older sample.
Get tutor helpright-arrow

Posted 7 months ago

Question
The average production cost for major movies is 6767 million dollars and the standard deviation is 2323 million dollars. Assume the production cost distribution is normal. Suppose that 4646 randomly selected major movies are researched. Answer the following questions. Give your answers in millions of dollars, not dollars. Round all answers to 44 decimal places where possible.\newlinea. What is the distribution of XX? \newlineX∼N(67,232)X \sim N(67, 23^2)\newlineb. What is the distribution of xˉ\bar{x}? \newlinexˉ∼N(67,(2346)2)\bar{x} \sim N\left(67, \left(\frac{23}{\sqrt{46}}\right)^2\right)\newlinec. For a single randomly selected movie, find the probability that this movie's production cost is between 6969 and 7373 million dollars. \newline232300\newlined. For the group of 4646 movies, find the probability that the average production cost is between 6969 and 7373 million dollars. 232344\newlinee. For part d), is the assumption of normal necessary?\newlineNo\newlineYes\newline232355
Get tutor helpright-arrow

Posted 7 months ago

Question
Chapter 33 - Homework\newlineSaved\newlineHelp\newlineExercise 33−51-51 (Algo) Multiproduct CVP Analysis (LO 33−4-4)\newline11.1111\newlinepoints\newlineSkIpped\newlineeBook\newlineHint\newlinePrint\newlineReferences\newlineGeorgeland Cycles makes and sells two models of electric bicycles. The Commuter (a folding model) sells for $2,503.00\$2,503.00 and the Tour\newlineX (a fat-tire trail model) sells for $4,503.00\$4,503.00. Unit variable costs for the Commuter are $1,753.00\$1,753.00 and for the Tour\newline-X$3,203.00\$3,203.00. Annual fixed costs at Georgeland are $488,050\$488,050. The marketing manager estimates that the annual mix of sales is 3030 percent Commuter model and 7070 percent Touring model.\newlineRequired:\newlinea. How many of each model ebike must Georgeland Cycles sell every year to break even?\newlineb. How many of each model ebike must Georgeland Cycles sell every year to earn operating profits of $102,150\$102,150 before taxes?\newlineComplete this question by entering your answers in the tabs below.\newlineRequired \newlineA\newlineRequired B\newlineHow many of each model ebike must Georgeland Cycles sell every year to break even?\newline\newlineCommuter\newlineTour-\newlineX\newline\newlineBreak-even ebikes\newline\newlineRequired \newlineB
Get tutor helpright-arrow

Posted 7 months ago

Question
55, 1010 and 11, n
Get tutor helpright-arrow

Posted 17 hours ago

View all (163)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant