Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

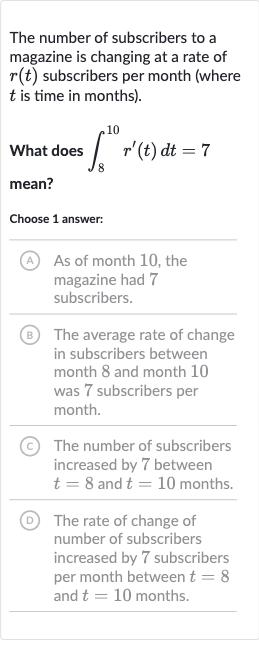
The number of subscribers to a magazine is changing at a rate of
r(t) subscribers per month (where
t is time in months).
What does
int_(8)^(10)r^(')(t)dt=7 mean?
Choose 1 answer:
(A) As of month 10 , the magazine had 7 subscribers.
(B) The average rate of change in subscribers between month 8 and month 10 was 7 subscribers per month.
(C) The number of subscribers increased by 7 between
t=8 and
t=10 months.
(D) The rate of change of number of subscribers increased by 7 subscribers per month between
t=8 and
t=10 months.

The number of subscribers to a magazine is changing at a rate of $r(t)$ subscribers per month (where $t$ is time in months). $\newline$ What does $\int_{8}^{10} r^{\prime}(t) d t=7$ mean? $\newline$ Choose $1$ answer: $\newline$ (A) As of month $10$ , the magazine had $7$ subscribers. $\newline$ (B) The average rate of change in subscribers between month $8$ and month $10$ was $7$ subscribers per month. $\newline$ (C) The number of subscribers increased by $7$ between $t=8$ and $t=10$ months. $\newline$ (D) The rate of change of number of subscribers increased by $7$ subscribers per month between $t=8$ and $t=10$ months.

View step-by-step help

View step-by-step help

Evaluate two-variable equations: word problems

Full solution

Q. The number of subscribers to a magazine is changing at a rate of

r(t)

subscribers per month (where

t

is time in months).

\newline

What does

\int_{8}^{10} r^{\prime}(t) d t=7

mean?

\newline

Choose

1

answer:

\newline

(A) As of month

10

, the magazine had

7

subscribers.

\newline

(B) The average rate of change in subscribers between month

8

and month

10

was

7

subscribers per month.

\newline

(C) The number of subscribers increased by

7

between

t=8

and

t=10

months.

\newline

(D) The rate of change of number of subscribers increased by

7

subscribers per month between

t=8

and

t=10

months.

Understand the expression: Understand the integral expression. $\newline$ The integral of $r'(t)$ from $8$ to $10$ represents the total change in the number of subscribers from month $8$ to month $10$ .
Interpret the result: Interpret the result of the integral. $\newline$ Since the integral of the rate of change of subscribers, $r'(t)$ , over the interval from $t=8$ to $t=10$ is equal to $7$ , this means that the total change in the number of subscribers over these two months is $7$ subscribers.
Match interpretation to options: Match the interpretation to the given options. $\newline$ The correct interpretation of the integral result is that the number of subscribers increased by $7$ between $t=8$ and $t=10$ months. This matches option (C).
Eliminate incorrect options: Eliminate other options based on the interpretation. $\newline$ Option (A) is incorrect because the integral does not provide information about the total number of subscribers at any point in time. $\newline$ Option (B) is incorrect because the integral gives the total change, not the average rate of change. $\newline$ Option (D) is incorrect because the integral gives the total change in subscribers, not the change in the rate of change.

More problems from Evaluate two-variable equations: word problems

Question

b(t)

gives the temperature (in degrees Celsius) of a pan of brownies by time

t

\newline

\int_{0}^{6} b^{\prime}(t) d t=93

\newline

1

\newline

t=6

minutes, the temperature of the brownies is

93

degrees Celsius.

\newline

t=6

minutes, the brownies have an instantaneous rate of temperature change of

93

degrees Celsius per minute.

\newline

(C) During the first six minutes, the temperature of the brownies increases an average of

93

degrees Celsius per minute.

\newline

(D) The temperature of the brownies increased by

93

degrees Celsius in the first six minutes.

Posted 9 months ago

Question

A grocery store receives a shipment of bananas. The percent of the shipment that is still suitable for sale is decreasing at a rate of

r(t)

percent of the original shipment per day (where

t

is the time in days). At

t=2

, the grocery store found

85 \%

of the shipment to be suitable for sale.

\newline

0.85+\int_{2}^{4} r(t) d t=0.6 \text { mean? }

\newline

1

\newline

(A) As of the fourth day,

60 \%

of the bananas suitable on the second day are still suitable.

\newline

(B) Between the second and fourth days,

60 \%

of the remaining bananas became unsuitable for sale per day.

\newline

(C) Between the second and fourth day, another

60 \%

of the bananas became unsuitable for sale.

\newline

(D) As of the fourth day,

60 \%

of the shipment was still suitable for sale.

Posted 9 months ago

Question

The number of people exposed to a certain illness is increasing at a rate of

r(t)

people per day (where

t

is the time in days). At

t=12

115

people exposed to the illness.

\newline

115+\int_{12}^{20} r(t) d t

\newline

1

\newline

(A) The change in the number of people exposed to the illness between days

12

20

\newline

(B) The change in the rate at which people are exposed to the illness between days

12

20

\newline

(C) The time it takes for

20

more people to be exposed to the illness

\newline

(D) The number of people exposed to the illness at

t=20

Posted 9 months ago

Question

The population of a town grows at a rate of

r(t)

people per year (where

t

is time in years). At

t=3

, the town's population was

1000

\newline

1000+\int_{3}^{8} r(t) d t=1500

\newline

1

\newline

(A) The town's population grew by

1500

t=3

t=8

\newline

(B) The town's population grew at a rate of

1500

people per year at

t=8

\newline

(C) The average rate at which the population grew between

t=3

t=8

1500

people per year.

\newline

t=8

, the town's population was

1500

Posted 9 months ago

Question

The value of a computer is decreasing at a rate that is proportional at any time to the value of the computer at that time.

\newline

The computer is worth

\$ 850

initially, and it is worth

\$ 306

2

\newline

How much will the computer be worth after

5

\newline

1

\newline

\$ 0

\newline

\$ 66

\newline

\$ 79

Posted 9 months ago

Question

11(1.022)^{t}

models the per capita gross domestic product (GDP) of the US, in thousands of dollars, as a function of the number of years since

1950

\newline

1

022

represent in this expression?

\newline

1

\newline

(A) The per capita GDP in the US was

\$ 1022

1950

\newline

(B) The maximum per capita GDP occurred

1

022

1950

\newline

(C) The per capita GDP in the US is multiplied by approximately

1

022

Posted 9 months ago

Question

Carbon dating involves the measurement of the amount of carbon

-14

in a sample. Archaeologists sometimes use carbon dating to estimate the number of years since an organism died. The function shows the ratio,

R(t)

-14

remaining in a sample to the original amount of carbon

-14

t

\newline

R(t)=2^{-0.00175 t}

\newline

If one sample was

3

times as old as another sample of the same material, how would the carbon

-14

ratios of the samples relate?

\newline

1

\newline

(A) The ratio of the older sample would be

3

times the ratio of the newer sample.

\newline

(B) The ratio of the newer sample would be

3

times the ratio of the older sample.

\newline

(C) The ratio of the older sample would be the cube of the ratio of the newer sample.

\newline

(D) The ratio of the newer sample would be the cube of the ratio of the older sample.

Posted 9 months ago

Question

D=1,874-0.55 t

\newline

D

, in meters, between an antarctic glacier and the coast

t

days after January

1

2010

is approximated by the equation. How does the distance between the glacier and the coast change over time?

\newline

1

\newline

(A) The glacier moves

0.55

meters per day closer to the shore.

\newline

(B) The glacier moves

1,874

meters per day closer to the shore.

\newline

(C) The glacier moves

0.55

meters per day further from the shore.

\newline

(D) The glacier moves

1,874

meters per day further from the shore.

Posted 8 months ago

Question

Derin's boyfriend in Japan is

\$0.19

per minute. The rate to call her family in Turkey is

\$0.12

per minute. Derin wants to spend at least

30

minutes calling her family in Turkey. Which of the following systems of inequalities best represents the relationship between

J

, the number of minutes Derin calls Japan, and

T

, the number of minutes Derin calls Turkey?

\newline

1

\newline

0.19J+0.12T \leq 25

\newline

T \leq 30

\newline

0.19J+0.12T \geq 25

\newline

T \leq 30

\newline

0.19J+0.12T \leq 25

\newline

T \geq 30

\newline

0.19J+0.12T \geq 25

\newline

T \geq 30

Posted 8 months ago

Question

You pick a card at random, put it back, and then pick another card at random.

\newline

4

\newline

5

\newline

6

\newline

7

\newline

What is the probability of picking a number greater than

5

and then picking a

4

\newline

Write your answer as a percentage.

Posted 1 month ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant