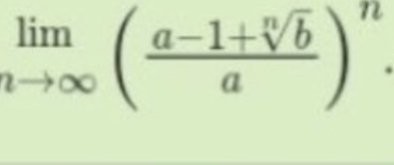AI tutor
Full solution
Q.
- Rewrite Limit Expression: First, let's rewrite the limit expression to make it clearer.
- Rewrite Inside Parentheses: Notice that the expression inside the parentheses can be rewritten as . So, we have
- Use Limit Property: Now, let's use the fact that when approaches infinity.Here, .
- Determine Value: As approaches infinity, approaches , so approaches .
- Calculate Final Limit: Therefore, the limit becomes .
- Final Answer: So, the final answer is .
More problems from Evaluate rational exponents
QuestionGet tutor help
QuestionGet tutor help