Let $f(x)=\frac{-x}{\ln ^{2}(x-1)}$ . $\newline$ Select the correct description of the one-sided limits of $f$ at $x=2$ . $\newline$ Choose $1$ answer: $\newline$ (A) $\lim _{x \rightarrow 2^{+}} f(x)=+\infty$ and $\lim _{x \rightarrow 2^{-}} f(x)=+\infty$ $\newline$ (B) $\lim _{x \rightarrow 2^{+}} f(x)=+\infty$ and $\lim _{x \rightarrow 2^{-}} f(x)=-\infty$ $\newline$ (C) $\lim _{x \rightarrow 2^{+}} f(x)=-\infty$ and $\lim _{x \rightarrow 2^{-}} f(x)=+\infty$ $\newline$ (D) $\lim _{x \rightarrow 2^{+}} f(x)=-\infty$ and $\lim _{x \rightarrow 2^{-}} f(x)=-\infty$

View step-by-step help

Home

Math Problems

Algebra 1

Compare linear, exponential, and quadratic growth

Full solution

Q. Let

f(x)=\frac{-x}{\ln ^{2}(x-1)}

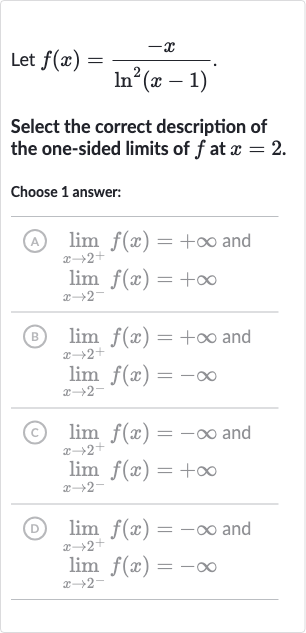
\newline

Select the correct description of the one-sided limits of

f

x=2

\newline

Choose

1

answer:

\newline

(A)

\lim _{x \rightarrow 2^{+}} f(x)=+\infty

and

\lim _{x \rightarrow 2^{-}} f(x)=+\infty

\newline

(B)

\lim _{x \rightarrow 2^{+}} f(x)=+\infty

and

\lim _{x \rightarrow 2^{-}} f(x)=-\infty

\newline

(C)

\lim _{x \rightarrow 2^{+}} f(x)=-\infty

and

\lim _{x \rightarrow 2^{-}} f(x)=+\infty

\newline

(D)

\lim _{x \rightarrow 2^{+}} f(x)=-\infty

and

\lim _{x \rightarrow 2^{-}} f(x)=-\infty

Analyze near $x = 2$ : Analyze the function near $x = 2$ . We have the function $f(x) = \frac{-x}{\ln^{2}(x-1)}$ . We need to consider the behavior of the function as $x$ approaches $2$ from the left ( $x \to 2^{-}$ ) and from the right ( $x \to 2^{+}$ ). We will look at the numerator and the denominator separately.
Numerator behavior at $x = 2$ : Consider the behavior of the numerator as $x$ approaches $2$ . The numerator is $-x$ . As $x$ approaches $2$ from either side, $-x$ approaches $-2$ . There is no ambiguity or complexity in the behavior of the numerator.
Denominator behavior at $x = 2$ : Consider the behavior of the denominator as $x$ approaches $2$ . The denominator is $\ln^{2}(x-1)$ , which is the square of the natural logarithm of $(x-1)$ . As $x$ approaches $2$ , $(x-1)$ approaches $1$ . The natural logarithm of $1$ is $x$ $0$ , so $\ln^{2}(x-1)$ approaches $x$ $0$ . We need to consider the sign of the natural logarithm as $x$ approaches $2$ from the left and right to determine the sign of the denominator.
Denominator sign at $x \to 2^{-}$ : Determine the sign of the denominator as $x$ approaches $2$ from the left. As $x$ approaches $2$ from the left ( $x \to 2^{-}$ ), $(x-1)$ is slightly less than $1$ . The natural logarithm of a number slightly less than $1$ is negative, so $\ln(x-1)$ is negative. Squaring a negative number gives a positive result, so $x$ $0$ is positive as $x$ approaches $2$ from the left.
Denominator sign at $x \to 2^{+}$ : Determine the sign of the denominator as $x$ approaches $2$ from the right. $\newline$ As $x$ approaches $2$ from the right ( $x \to 2^{+}$ ), $(x-1)$ is slightly more than $1$ . The natural logarithm of a number slightly more than $1$ is positive, so $\ln(x-1)$ is positive. Squaring a positive number gives a positive result, so $x$ $0$ is positive as $x$ approaches $2$ from the right.
Combine for one-sided limits: Combine the behavior of the numerator and denominator to find the one-sided limits. $\newline$ Since the numerator approaches $-2$ and the denominator approaches $0$ with a positive sign from both sides, the fraction $\frac{-x}{\ln^{2}(x-1)}$ will approach negative infinity from both sides. This is because a negative number divided by a positive number that is getting closer and closer to zero will result in a number that is getting more and more negative.