Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

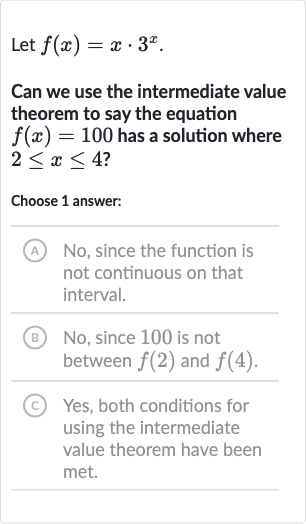
Let
f(x)=x*3^(x).
Can we use the intermediate value theorem to say the equation
f(x)=100 has a solution where
2 <= x <= 4 ?
Choose 1 answer:
(A) No, since the function is not continuous on that interval.
(B) No, since 100 is not between
f(2) and
f(4).
(C) Yes, both conditions for using the intermediate value theorem have been met.

Let $f(x)=x \cdot 3^{x}$ . $\newline$ Can we use the intermediate value theorem to say the equation $f(x)=100$ has a solution where $2 \leq x \leq 4$ ? $\newline$ Choose $1$ answer: $\newline$ (A) No, since the function is not continuous on that interval. $\newline$ (B) No, since $100$ is not between $f(2)$ and $f(4)$ . $\newline$ (C) Yes, both conditions for using the intermediate value theorem have been met.

View step-by-step help

View step-by-step help

Write a quadratic function from its x-intercepts and another point

Full solution

Q. Let

f(x)=x \cdot 3^{x}

.

\newline

Can we use the intermediate value theorem to say the equation

f(x)=100

has a solution where

2 \leq x \leq 4

?

\newline

Choose

1

answer:

\newline

(A) No, since the function is not continuous on that interval.

\newline

(B) No, since

100

is not between

f(2)

and

f(4)

.

\newline

(C) Yes, both conditions for using the intermediate value theorem have been met.

Check Continuity: We need to check if the function $f(x) = x \cdot 3^x$ is continuous on the interval $[2, 4]$ . Since $f(x)$ is a product of a polynomial function $x$ and an exponential function $3^x$ , both of which are continuous everywhere, $f(x)$ is also continuous on the interval $[2, 4]$ .
Calculate $f(2)$ : Next, we need to calculate the value of $f(x)$ at the endpoints of the interval to see if $100$ lies between $f(2)$ and $f(4)$ . First, we calculate $f(2) = 2 \times 3^2 = 2 \times 9 = 18$ .
Calculate $f(4)$ : Now, we calculate $f(4) = 4 \times 3^4 = 4 \times 81 = 324$ .
Apply Intermediate Value Theorem: We observe that $100$ is between $f(2) = 18$ and $f(4) = 324$ . Therefore, by the intermediate value theorem, since $f(x)$ is continuous on $[2, 4]$ and $100$ is between $f(2)$ and $f(4)$ , there must be some value $c$ in the interval $[2, 4]$ such that $f(2) = 18$ $0$ .

More problems from Write a quadratic function from its x-intercepts and another point

Question

h

is defined over the real numbers. This table gives a few values of

h

\newline

\begin{tabular}{lllll}

\newline

x

-6

1

-6

01

-6

001

-5

9

\newline

h(x)

-0

25

-0

74

-0

98

-1

0

\newline

\newline

What is a reasonable estimate for

\lim _{x \rightarrow-6} h(x)

\newline

1

\newline

-6

\newline

-2

\newline

-1

\newline

(D) The limit doesn't exist

Posted 10 months ago

Question

What is the amplitude of

\newline

g(x)=-2 \sin \left(\frac{\pi}{2} x-3\right)+5 ?

\newline

Posted 10 months ago

Question

What is the amplitude of

y=5 \sin (4 x-2)-3

\newline

Posted 10 months ago

Question

What is the amplitude of

y=-3 \cos (\pi x+2)-6 ?

\newline

Posted 10 months ago

Question

What is the amplitude of

y=3 \sin (2 x-1)+4

\newline

Posted 10 months ago

Question

What is the period of the function

h(x)=-3 \cos (\pi x+2)-6 ?

\newline

Give an exact value.

\newline

Posted 10 months ago

Question

What is the period of the function

\newline

h(x)=5 \sin (4 x-2)-3 \text { ? }

\newline

Give an exact value.

\newline

Posted 10 months ago

Question

What is the period of the function

g(x)=2 \cos (7 x+5)+1 ?

\newline

Give an exact value.

\newline

Posted 10 months ago

Question

What is the period of the function

f(x)=3 \sin (2 x-1)+4

\newline

Give an exact value.

\newline

Posted 10 months ago

Question

What is the period of the function

f(x)=-4 \cos (5 x-9)-7

\newline

Give an exact value.

\newline

Posted 10 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant