Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

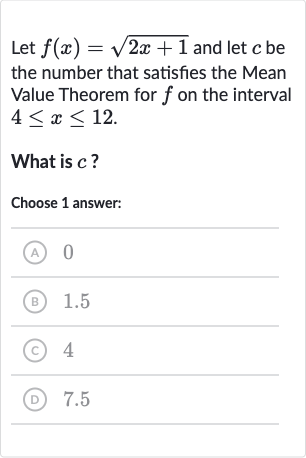
Let
f(x)=sqrt(2x+1) and let
c be the number that satisfies the Mean Value Theorem for
f on the interval
4 <= x <= 12.
What is
c ?
Choose 1 answer:
(A) 0
(B) 1.5
(C) 4
(D) 7.5

Let $f(x)=\sqrt{2 x+1}$ and let $c$ be the number that satisfies the Mean Value Theorem for $f$ on the interval $4 \leq x \leq 12$ . $\newline$ What is $c$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $0$ $\newline$ (B) $1$ . $5$ $\newline$ (C) $4$ $\newline$ (D) $7$ . $5$

View step-by-step help

View step-by-step help

Solve quadratic inequalities

Full solution

Q. Let

f(x)=\sqrt{2 x+1}

and let

c

be the number that satisfies the Mean Value Theorem for

f

on the interval

4 \leq x \leq 12

.

\newline

What is

c

?

\newline

Choose

1

answer:

\newline

(A)

0

\newline

(B)

1

.

5

\newline

(C)

4

\newline

(D)

7

.

5

Understand Mean Value Theorem: Understand the Mean Value Theorem (MVT). The MVT states that if a function $f$ is continuous on the closed interval $[a, b]$ and differentiable on the open interval $(a, b)$ , then there exists at least one number $c$ in $(a, b)$ such that $f'(c) = \frac{f(b) - f(a)}{b - a}$ .
Apply MVT to Function: Apply the MVT to the function $f(x) = \sqrt{2x + 1}$ on the interval $[4, 12]$ . $\newline$ First, calculate $f(4)$ and $f(12)$ . $\newline$ $f(4) = \sqrt{2\cdot4 + 1} = \sqrt{9} = 3$ $\newline$ $f(12) = \sqrt{2\cdot12 + 1} = \sqrt{25} = 5$
Calculate Difference Quotient: Calculate the difference quotient $(f(b) - f(a)) / (b - a)$ . $(f(12) - f(4)) / (12 - 4) = (5 - 3) / (12 - 4) = 2 / 8 = 1/4$
Find Derivative of $f(x)$ : Find the derivative of $f(x)$ .
$f'(x) = \frac{d}{dx} [\sqrt{2x + 1}]$
To differentiate $\sqrt{2x + 1}$ , use the chain rule.
$f'(x) = \frac{1}{2\sqrt{2x + 1}} \cdot \frac{d}{dx} [2x + 1]$
$f'(x) = \frac{1}{2\sqrt{2x + 1}} \cdot 2$
$f'(x) = \frac{1}{\sqrt{2x + 1}}$
Set Derivative Equal to Quotient: Set the derivative equal to the difference quotient and solve for $c$ . $\frac{1}{\sqrt{2c + 1}} = \frac{1}{4}$ Cross-multiply to solve for $c$ . $4 = \sqrt{2c + 1}$ Square both sides to eliminate the square root. $16 = 2c + 1$ Subtract $1$ from both sides. $15 = 2c$ Divide by $2$ . $c = \frac{15}{2}$ $c = 7.5$

More problems from Solve quadratic inequalities

Question

-10 x-3 \geq 8 x+4

\newline

Which of the following best describes the solutions to the inequality shown?

\newline

1

\newline

x \leq-\frac{7}{18}

\newline

x \leq-\frac{7}{2}

\newline

x \leq-\frac{1}{18}

\newline

x \geq-\frac{7}{18}

Posted 10 months ago

Question

-12 x<-72

\newline

Which of the following best describes the solutions to the inequality shown?

\newline

1

\newline

x<6

\newline

x>6

\newline

x<\frac{1}{6}

\newline

x>\frac{1}{6}

Posted 10 months ago

Question

8 x+6<4 x+10

\newline

Which of the following best describes the solutions to the inequality shown?

\newline

1

\newline

x<\frac{1}{3}

\newline

x<4

\newline

x<1

\newline

x>1

Posted 10 months ago

Question

6 x-2<2 x+3

\newline

Which of the following best describes the solutions to the inequality shown?

\newline

1

\newline

x<\frac{5}{4}

\newline

x>\frac{5}{4}

\newline

x<\frac{1}{4}

\newline

x<\frac{5}{8}

Posted 10 months ago

Question

16<-4 x

\newline

Which of the following best describes the solutions to the inequality shown?

\newline

1

\newline

x<-4

\newline

x>-4

\newline

x<-\frac{1}{4}

\newline

x>-\frac{1}{4}

Posted 10 months ago

Question

\lim _{x \rightarrow 4} \frac{2-\sqrt{4 x-12}}{x-4}

\newline

1

\newline

2

\newline

1

\newline

-1

\newline

(D) The limit doesn't exist

Posted 9 months ago

Question

\lim _{x \rightarrow 2} \frac{x^{4}-4 x^{3}+4 x^{2}}{x-2}

\newline

1

\newline

-4

\newline

0

\newline

4

\newline

(D) The limit doesn't exist

Posted 9 months ago

Question

f

be a continuous function on the closed interval

[-5,0]

f(-5)=0

f(0)=5

\newline

Which of the following is guaranteed by the Intermediate Value Theorem?

\newline

1

\newline

f(c)=-2

for at least one

c

0

5

\newline

f(c)=2

for at least one

c

0

5

\newline

f(c)=-2

for at least one

c

-5

0

\newline

f(c)=2

for at least one

c

-5

0

Posted 9 months ago

Question

g(x)=\tan (x)

\newline

Can we use the intermediate value theorem to say the equation

g(x)=0

has a solution where

\frac{\pi}{4} \leq x \leq \frac{3 \pi}{4}

\newline

1

\newline

(A) No, since the function is not continuous on that interval.

\newline

0

g\left(\frac{\pi}{4}\right)

g\left(\frac{3 \pi}{4}\right)

\newline

(C) Yes, both conditions for using the intermediate value theorem have been met.

Posted 9 months ago

Question

g(x)=\cos (x)

\newline

Can we use the intermediate value theorem to say the equation

g(x)=0.8

has a solution where

0 \leq x \leq \frac{\pi}{2}

\newline

1

\newline

(A) No, since the function is not continuous on that interval.

\newline

0

8

g(0)

g\left(\frac{\pi}{2}\right)

\newline

(C) Yes, both conditions for using the intermediate value theorem have been met.

Posted 9 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant