Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Let f(x)=(3)/(x). Select the correct description of the one-sided limits of f at x=0. Choose 1 answer: (A) lim_(x rarr0^(+))f(x)=+oo and lim_(x rarr0^(-))f(x)=+oo (B) lim_(x rarr0^(+))f(x)=+oo and lim_(x rarr0^(-))f(x)=-oo (c) lim_(x rarr0^(+))f(x)=-oo and lim_(x rarr0^(-))f(x)=+oo (D) lim_(x rarr0^(+))f(x)=-oo and lim_(x rarr0^(-))f(x)=-oo

Let f(x)=3x f(x)=\frac{3}{x} .\newlineSelect the correct description of the one-sided limits of f f at x=0 x=0 .\newlineChoose 11 answer:\newline(A) lim⁡x→0+f(x)=+∞ \lim _{x \rightarrow 0^{+}} f(x)=+\infty and lim⁡x→0−f(x)=+∞ \lim _{x \rightarrow 0^{-}} f(x)=+\infty \newline(B) lim⁡x→0+f(x)=+∞ \lim _{x \rightarrow 0^{+}} f(x)=+\infty and lim⁡x→0−f(x)=−∞ \lim _{x \rightarrow 0^{-}} f(x)=-\infty \newline(C) lim⁡x→0+f(x)=−∞ \lim _{x \rightarrow 0^{+}} f(x)=-\infty and lim⁡x→0−f(x)=+∞ \lim _{x \rightarrow 0^{-}} f(x)=+\infty \newline(D) lim⁡x→0+f(x)=−∞ \lim _{x \rightarrow 0^{+}} f(x)=-\infty and lim⁡x→0−f(x)=−∞ \lim _{x \rightarrow 0^{-}} f(x)=-\infty

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Compare linear and exponential growthright chevron icon

Full solution

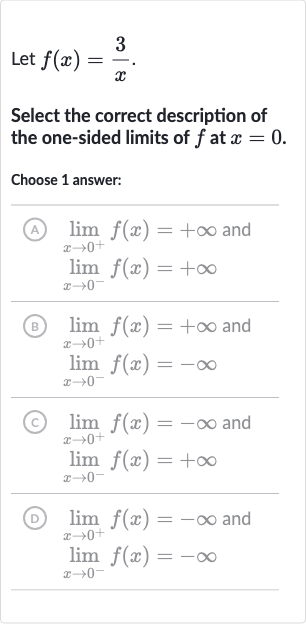
Q. Let f(x)=3x f(x)=\frac{3}{x} .\newlineSelect the correct description of the one-sided limits of f f at x=0 x=0 .\newlineChoose 11 answer:\newline(A) lim⁡x→0+f(x)=+∞ \lim _{x \rightarrow 0^{+}} f(x)=+\infty and lim⁡x→0−f(x)=+∞ \lim _{x \rightarrow 0^{-}} f(x)=+\infty \newline(B) lim⁡x→0+f(x)=+∞ \lim _{x \rightarrow 0^{+}} f(x)=+\infty and lim⁡x→0−f(x)=−∞ \lim _{x \rightarrow 0^{-}} f(x)=-\infty \newline(C) lim⁡x→0+f(x)=−∞ \lim _{x \rightarrow 0^{+}} f(x)=-\infty and lim⁡x→0−f(x)=+∞ \lim _{x \rightarrow 0^{-}} f(x)=+\infty \newline(D) lim⁡x→0+f(x)=−∞ \lim _{x \rightarrow 0^{+}} f(x)=-\infty and lim⁡x→0−f(x)=−∞ \lim _{x \rightarrow 0^{-}} f(x)=-\infty
  1. Analyze behavior of f(x)f(x) as xx approaches 0+0+: Analyze the behavior of the function f(x)=3xf(x) = \frac{3}{x} as xx approaches 00 from the positive side (x→0+x \rightarrow 0^+).\newlineAs xx gets closer to 00 from the positive side, the value of f(x)f(x) becomes larger and larger because the denominator of the fraction is getting smaller. This means that the function is approaching positive infinity.
  2. Calculate limit of f(x)f(x) as xx approaches 0+0+: Calculate the limit of f(x)f(x) as xx approaches 00 from the positive side.\newlinelim⁡x→0+f(x)=lim⁡x→0+(3x)=+∞\lim_{x \to 0^+} f(x) = \lim_{x \to 0^+} \left(\frac{3}{x}\right) = +\infty
  3. Analyze behavior of f(x)f(x) as xx approaches 0−0-: Analyze the behavior of the function f(x)=3xf(x) = \frac{3}{x} as xx approaches 00 from the negative side (x→0−x \rightarrow 0^-).\newlineAs xx gets closer to 00 from the negative side, the value of f(x)f(x) becomes more negative and larger in magnitude because the denominator of the fraction is getting smaller and is negative. This means that the function is approaching negative infinity.
  4. Calculate limit of f(x)f(x) as xx approaches 0−0-: Calculate the limit of f(x)f(x) as xx approaches 00 from the negative side.\newlinelim⁡x→0−f(x)=lim⁡x→0−(3x)=−∞\lim_{x \to 0^-} f(x) = \lim_{x \to 0^-} \left(\frac{3}{x}\right) = -\infty
  5. Combine results from Step 22 and Step 44: Combine the results from Step 22 and Step 44 to answer the question prompt.\newlineThe one-sided limits of the function f(x)=3xf(x) = \frac{3}{x} as xx approaches 00 are:\newlinelim⁡x→0+f(x)=+∞\lim_{x \to 0^+} f(x) = +\infty and lim⁡x→0−f(x)=−∞\lim_{x \to 0^-} f(x) = -\infty

More problems from Compare linear and exponential growth

Question
Jill bought a used motorcycle from a seller online for $1,200. The seller will charge her $5 a day to store the motorcycle at his house until she is able to pick it up. You can use a function to describe the total amount of money Jill will owe the seller if she waits xx days to pick up the motorcycle.\newlineWrite an equation for the function. If it is linear, write it in the form g(x)=mx+bg(x) = mx + b. If it is exponential, write it in the form g(x)=a(b)xg(x) = a(b)^x.\newlineg(x)=‾g(x) = \underline{\hspace{3em}}
Get tutor helpright-arrow

Posted 7 months ago

Question
How does f(t)=−2t−7f(t)=-2t-7 change over the interval from t=−7t=-7 to t=−6t=-6?\newlineChoices:\newline[f(t) decreases by 2]\left[\text{f(t) decreases by } 2\right]\newline[f(t) increases by 2]\left[\text{f(t) increases by } 2\right]\newline[f(t) increases by 200%]\left[\text{f(t) increases by } 200\%\right]\newline[f(t) decreases by a factor of 2]\left[\text{f(t) decreases by a factor of } 2\right]
Get tutor helpright-arrow

Posted 8 months ago

Question
How does g(t)=9tg(t)=9^t change over the interval from t=1t=1 to t=3t=3?\newlineChoices: \newline[g(t) decreases by a factor of 81]\left[\text{g(t) decreases by a factor of } 81\right]\newline[g(t) increases by a factor of 81]\left[\text{g(t) increases by a factor of } 81\right]\newline[g(t) increases by 18%]\left[\text{g(t) increases by } 18\%\right]\newline[g(t) decreases by 9%]\left[\text{g(t) decreases by } 9\%\right]
Get tutor helpright-arrow

Posted 7 months ago

Question
Both of these functions grow as xx gets larger and larger. Which function eventually exceeds the other?\newline Choices:\newline(A)f(x)=8x+3.3(A)f(x) = 8x + 3.3\newline(B)g(x)=3.3x−5(B)g(x) = 3.3^x - 5
Get tutor helpright-arrow

Posted 8 months ago

Question
Both of these functions grow as x x gets larger and larger. Which function eventually exceeds the other?\newlineChoices:\newline(A) f(x)=2x+9(A) \ f(x) = 2x + 9 \newline(B) g(x)=2x(B)\ g(x) = 2^x
Get tutor helpright-arrow

Posted 8 months ago

Question
The functions f(x) f(x) and g(x) g(x) are differentiable. \newlineThe function h(x) h(x) is defined as: h(x)=g(x)f(x) h(x)=\frac{g(x)}{f(x)} \newlineIf f(8)=1 f(8)=1 , f′(8)=−6 f'(8)=-6 , g(8)=8 g(8)=8 , and g′(8)=−10 g'(8)=-10 , what is h′(8) h'(8) ? \newlineSimplify any fractions. \newlineh′(8)= h'(8)= ______
Get tutor helpright-arrow

Posted 8 months ago

Question
The functions p(x) p(x) and q(x) q(x) are differentiable. \newlineThe function r(x) r(x) is defined as: r(x)=p(x)q(x) r(x)= \frac{p(x)}{q(x)} \newlineIf p(3)=2 p(3)= 2 , p′(3)=4 p'(3)= 4 , q(3)=6 q(3)= 6 , and q′(3)=9 q'(3)= 9 , what is r′(3) r'(3) ? \newlineSimplify any fractions. \newliner′(3)= r'(3)= _____
Get tutor helpright-arrow

Posted 9 months ago

Question
The functions u(x) u(x) and v(x) v(x) are differentiable. \newlineThe function w(x) w(x) is defined as: w(x)=u(x)v(x) w(x)= \frac{u(x)}{v(x)} \newlineIf u(5)=3 u(5)= 3 , u′(5)=−2 u'(5)= -2 , v(5)=7 v(5)= 7 , and v′(5)=1 v'(5)= 1 , what is w′(5) w'(5) ? \newlineSimplify any fractions. \newlinew′(5)= w'(5)= _____
Get tutor helpright-arrow

Posted 9 months ago

Question
The functions a(x) a(x) and b(x) b(x) are differentiable. \newlineThe function c(x) c(x) is defined as: c(x)=a(x)b(x) c(x)= \frac{a(x)}{b(x)} \newlineIf a(2)=4 a(2)= 4 , a′(2)=5 a'(2)= 5 , b(2)=1 b(2)= 1 , and b′(2)=−3 b'(2)= -3 , what is c′(2) c'(2) ? \newlineSimplify any fractions. \newlinec′(2)= c'(2)= _____
Get tutor helpright-arrow

Posted 9 months ago

Question
The functions m(x) m(x) and n(x) n(x) are differentiable. \newlineThe function o(x) o(x) is defined as: o(x)=m(x)n(x) o(x)= \frac{m(x)}{n(x)} \newlineIf m(7)=2 m(7)= 2 , m′(7)=−1 m'(7)= -1 , n(7)=4 n(7)= 4 , and n′(7)=8 n'(7)= 8 , what is o′(7) o'(7) ? \newlineSimplify any fractions. \newlineo′(7)= o'(7)= _____
Get tutor helpright-arrow

Posted 9 months ago

View all (345)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant